 |
Завдання на період з 16.05 по 20.05 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 20.05
Тема : "Повторення теми : «Трикутники. Ознаки рівності трикутників»"
Переглянути відео :https://www.youtube.com/watch?v=-eT9EWChXOY
Опрацювати матеріал :Медіана трикутника — це відрізок, що сполучає вершину трикутника із серединою протилежної сторони.Для побудови медіани необхідно виконати такі дії:
1) Знайти середину сторони.
2) З'єднати точку, яка є серединою сторони трикутника, з протилежною вершиною трикутника. Це і буде медіана. 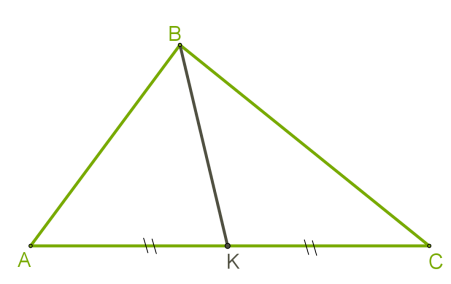 Зверни увагу!У трикутнику можна побудувати три медіани, які перетинаються в одній точці і мають такі властивості:
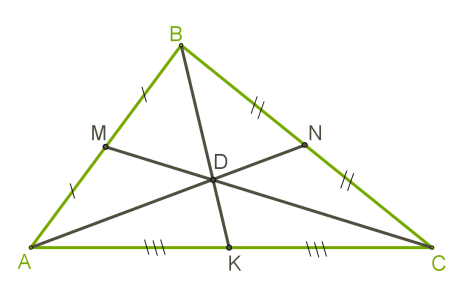
Зверни увагу!У трикутнику можна побудувати три медіани, які перетинаються в одній точці і мають такі властивості:- Медіани трикутника перетинаються в точці, яка є його центром мас.
- Медіани трикутника зображені чорним кольором.
- Медіана поділяє трикутник на два трикутники з рівними площами (рівновеликі), а три проведені медіани — на шість рівновеликих.
- В точці перетину медіани трикутника діляться у відношенні 2:1, починаючи з вершини трикутника.
- Медіана прямокутного трикутника, проведена до гіпотенузи, дорівнює половині гіпотенузи.
- В рівнобедреному трикутнику медіана кута, протилежного до основи трикутника, є його бісектрисою та висотою.
 Бісектриса трикутника — це відрізок бісектриси кута трикутника, що сполучає вершину з точкою на протилежній стороні.Для побудови бісектриси необхідно виконати такі дії:
Бісектриса трикутника — це відрізок бісектриси кута трикутника, що сполучає вершину з точкою на протилежній стороні.Для побудови бісектриси необхідно виконати такі дії:
1) Побудувати бісектрису кута трикутника (бісектриса кута — це промінь, що виходить із вершини кута й ділить його на дві рівні частини).
2) Знайти точку перетину бісектриси кута трикутника з протилежною стороною.
3) З'єднати вершину трикутника з точкою перетину бісектриси кута трикутника з протилежною стороною — цей відрізок і буде бісектрисою трикутника. 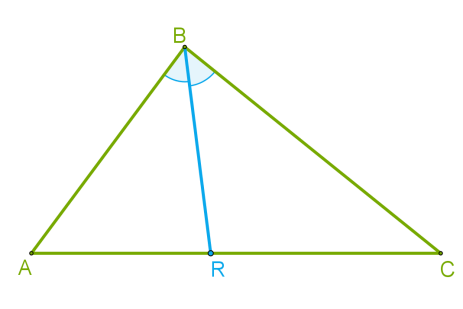 Зверни увагу!У трикутника є три бісектриси, які перетинаються в одній точці і мають такі властивості:
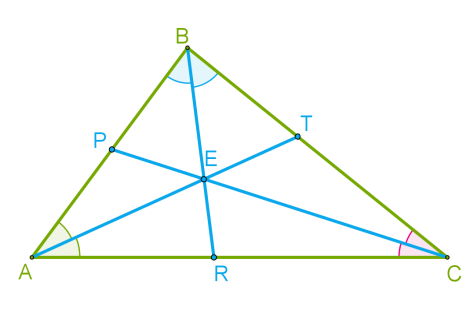
Зверни увагу!У трикутника є три бісектриси, які перетинаються в одній точці і мають такі властивості:- Бісектриси внутрішніх кутів трикутника перетинаються в одній точці — інцентрі — центрі вписаного в цей трикутник кола.
- Бісектриси трикутника зображені голубим кольором.
- Бісектриса внутрішнього кута трикутника ділить протилежну сторону у відношенні, рівному відношенню двох прилеглих сторін.
- Якщо в трикутнику дві бісектриси рівні, то трикутник — рівнобедрений.
- В рівнобедреному трикутнику бісектриса кута, протилежного до основи трикутника, є медіаною та висотою.
- Відстані від сторін кута до будь-якої точки бісектриси однакові.
 Висота трикутника — це перпендикуляр, опущений із вершини трикутника до прямої, що містить його протилежну сторону.Для побудови висоти необхідно виконати такі дії:
Висота трикутника — це перпендикуляр, опущений із вершини трикутника до прямої, що містить його протилежну сторону.Для побудови висоти необхідно виконати такі дії:
1) провести пряму, яка містить одну зі сторін трикутника (у разі, якщо проводиться висота з вершини гострого кута в тупокутному трикутнику);
2) із вершини, що лежить навпроти проведеної прямої, опустити до неї перпендикуляр (перпендикуляр — це відрізок, проведений із точки до прямої, який утворює з нею кут величиною 90° ). Це і буде висота.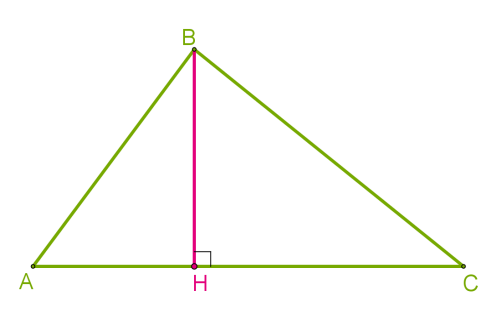 Так само, як медіани і бісектриси, трикутник має три висоти, які перетинаються в одній точці.
Так само, як медіани і бісектриси, трикутник має три висоти, які перетинаються в одній точці.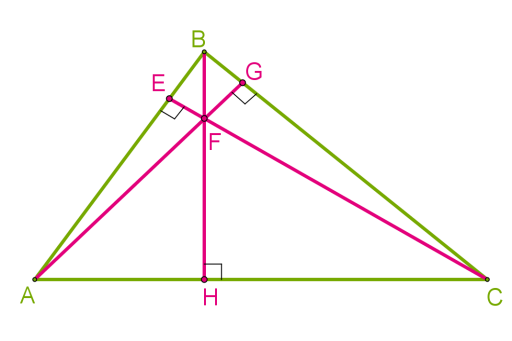 Точку перетину висот трикутника називають ортоцентром. В гострокутному він знаходиться всередині трикутника.
Точку перетину висот трикутника називають ортоцентром. В гострокутному він знаходиться всередині трикутника.
Якщо трикутник має прямий кут, то сторони, що утворюють прямий кут, можна назвати висотами, оскільки вони перпендикулярні одна до іншої. Точкою перетину висот є спільна вершина перпендикулярних сторін. Отже, в прямокутному трикутнику ортоцентр збігається з вершиною прямого кута. 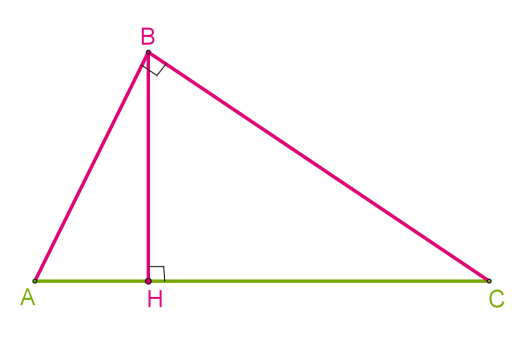 Якщо трикутник має тупий кут, то висоти, опущені з вершин гострих кутів, знаходитимуться за межами трикутника. Прямі, на яких розташовані висоти, перетинатимуться за трикутником. Отже, в тупокутному трикутнику ортоцентр лежить поза межами трикутника.
Якщо трикутник має тупий кут, то висоти, опущені з вершин гострих кутів, знаходитимуться за межами трикутника. Прямі, на яких розташовані висоти, перетинатимуться за трикутником. Отже, в тупокутному трикутнику ортоцентр лежить поза межами трикутника. 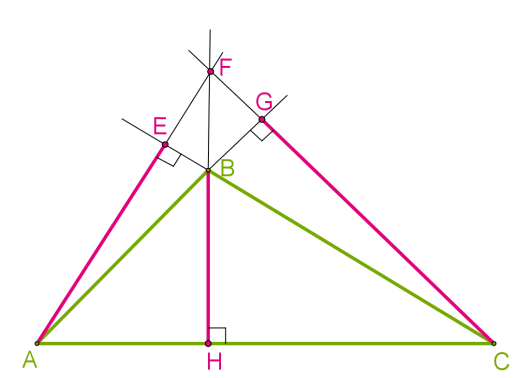 Зверни увагу!Якщо з однієї й тієї самої вершини провести медіану, бісектрису й висоту, то медіана виявиться найдовшим відрізком, а висота — найкоротшим.
Зверни увагу!Якщо з однієї й тієї самої вершини провести медіану, бісектрису й висоту, то медіана виявиться найдовшим відрізком, а висота — найкоротшим.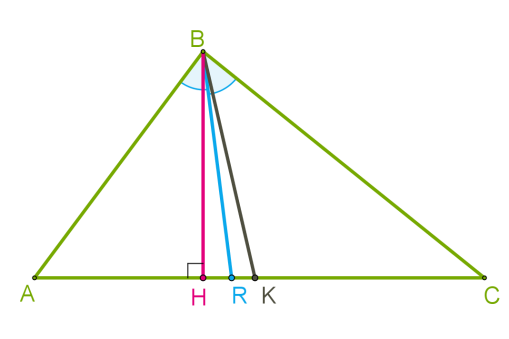 Зверни увагу!Кожний трикутник має три висоти, три медіани й три бісектриси.
Зверни увагу!Кожний трикутник має три висоти, три медіани й три бісектриси.
Довжини сторін трикутника, протилежних кутам А, В, С, позначають відповідно а, b, с. Довжини висот позначають ha , hb , hc , медіан — ma , mb , mc , бісектрис — la , lb , lc . Індекс показує, до якої сторони проведено відрізок. Це означає:- Проти кута
А лежить сторона а. - До сторони
а проведено висоту ha , медіану ma і бісектрису la .
всі ознаки рівності трикутників: 1. Якщо дві сторони і кут між ними одного трикутника відповідно дорівнюють двом сторонам і куту між ними іншого трикутника, то такі трикутники рівні.
2. Якщо сторона і два прилеглі до неї кути одного трикутника відповідно дорівнюють стороні та двом прилеглим до неї кутам іншого трикутника, то такі трикутники рівні.
3. Якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам іншого трикутника, то такі трикутники рівні.
Сума кутів трикутникаСума кутів трикутника дорівнює 180°. 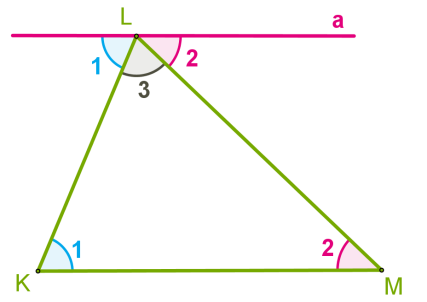 Доведення Розглянемо довільний трикутник
Доведення Розглянемо довільний трикутник KLM і доведемо, що ∠ K+ ∠ L + ∠ M= 180° 1. Проведемо через вершину L пряму a, паралельну стороні KM.
2. Кути, позначені цифрою 1, є внутрішніми різносторонніми кутами при перетині паралельних прямих a і KM січною KL. 3. Кути, позначені цифрою 2, — внутрішніми різносторонніми кутами при перетині тих самих паралельних прямих січною ML. 4. Очевидно, що сума кутів 1, 2 і 3 дорівнює розгорнутому куту з вершиною L, тобто:
∠ 1+ ∠ 2 + ∠ 3= 180° або ∠ K+ ∠ L + ∠ M= 180° Теорему доведено. Зверни увагу!Висновки з теореми про суму кутів трикутника
Висновок 1. Сума гострих кутів прямокутного трикутника дорівнює 90° . Висновок 2. У рівнобедреному прямокутному трикутнику кожен гострий кут дорівнює 45° . Висновок 3. У будь-якому трикутнику або всі кути гострі, або два кути гострі, а третій тупий або прямий.Зовнішній кут трикутникаЗовнішнім кутом трикутника називається кут, суміжний із внутрішнім кутом даного трикутника.
Теорема (про зовнішній кут трикутника)
Зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів, не суміжних із ним.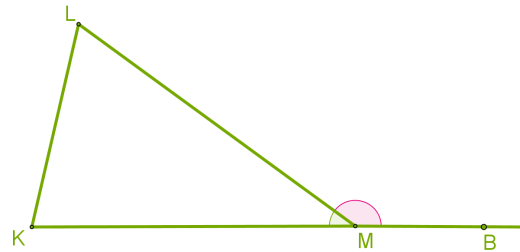 Доведення Із рівностей
Доведення Із рівностей ∠ KML + ∠ BML = 180° і ∠ K+ ∠ L + ∠ KML= 180° отримуємо, що: ∠ BML= ∠ K + ∠ L Наслідок
Сума зовнішніх кутів трикутника, взятих по одному при кожній вершині, дорівнює 360°.Гострокутний, прямокутний і тупокутний трикутникиЯк свідчить четвертий висновок із теореми про суму кутів трикутника, можна виокремити три види трикутників залежно від кутів. 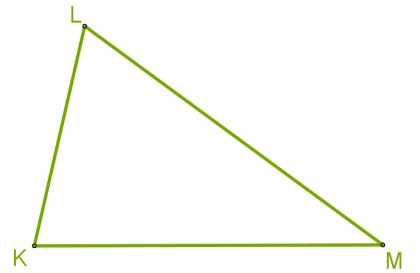 У трикутника
У трикутника KLM усі кути гострі. 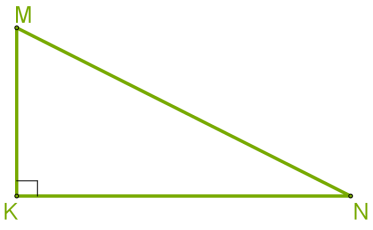 У трикутника
У трикутника KLM кут K=90 ° . У прямокутного трикутника сторона, що лежить навпроти прямого кута, називається гіпотенузою, а дві інші сторони — катетами. На рисунку MN — гіпотенуза, KN і KM — катети. 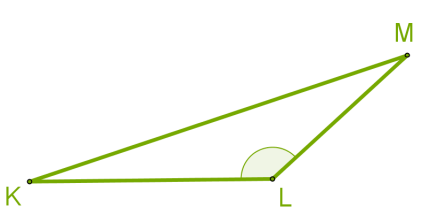 У трикутника
У трикутника KLM один кут тупий.

- Медіани трикутника перетинаються в точці, яка є його центром мас.
- Медіани трикутника зображені чорним кольором.
- Медіана поділяє трикутник на два трикутники з рівними площами (рівновеликі), а три проведені медіани — на шість рівновеликих.
- В точці перетину медіани трикутника діляться у відношенні 2:1, починаючи з вершини трикутника.
- Медіана прямокутного трикутника, проведена до гіпотенузи, дорівнює половині гіпотенузи.
- В рівнобедреному трикутнику медіана кута, протилежного до основи трикутника, є його бісектрисою та висотою.


- Бісектриси внутрішніх кутів трикутника перетинаються в одній точці — інцентрі — центрі вписаного в цей трикутник кола.
- Бісектриси трикутника зображені голубим кольором.
- Бісектриса внутрішнього кута трикутника ділить протилежну сторону у відношенні, рівному відношенню двох прилеглих сторін.
- Якщо в трикутнику дві бісектриси рівні, то трикутник — рівнобедрений.
- В рівнобедреному трикутнику бісектриса кута, протилежного до основи трикутника, є медіаною та висотою.
- Відстані від сторін кута до будь-якої точки бісектриси однакові.



Якщо трикутник має прямий кут, то сторони, що утворюють прямий кут, можна назвати висотами, оскільки вони перпендикулярні одна до іншої. Точкою перетину висот є спільна вершина перпендикулярних сторін. Отже, в прямокутному трикутнику ортоцентр збігається з вершиною прямого кута.



- Проти кута
А лежить сторонаа. - До сторони
а проведено висотуha , медіануma і бісектрисуla .

Теорема (про зовнішній кут трикутника)
Зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів, не суміжних із ним.

Сума зовнішніх кутів трикутника, взятих по одному при кожній вершині, дорівнює 360°.



Домашнє завдання : параграф 7,8, 11 повторити, № 675, 679 письмово
Дата 17.05
Тема : "Повторення теми : «Взаємне розміщення прямих на площині»"
Теорія:
 Визначення та доведення ознак паралельності прямих на площиніДві різні прямі, що лежать на одній площині, мають лише одну спільну точку, або не мають жодної спільної точки.У першому випадку говорять, що прямі перетинаються, у другому — що прямі не перетинаються.Дві прямі
Визначення та доведення ознак паралельності прямих на площиніДві різні прямі, що лежать на одній площині, мають лише одну спільну точку, або не мають жодної спільної точки.У першому випадку говорять, що прямі перетинаються, у другому — що прямі не перетинаються.Дві прямі a і b на площині, які не перетинаються, називаються паралельними і позначаються a∥b . Зверни увагу!Якщо розглядати прямі, які не лежать на одній площині, то можлива ситуація, що прямі не перетинаються, але й не є паралельними. Такі прямі називаються мимобіжними. Два відрізки називаються паралельними, якщо вони лежать на паралельних прямих.Аксіома паралельних прямих (аксіома Евкліда)
Два відрізки називаються паралельними, якщо вони лежать на паралельних прямих.Аксіома паралельних прямих (аксіома Евкліда)
Через точку, що не лежить на даній прямій, можна провести пряму, паралельну даній, і до того ж тільки одну.Ознаки паралельності прямих на площині.1. Дві прямі, паралельні третій, паралельні між собою.2. Якщо дві прямі на площині перпендикулярні до однієї й тієї самої прямої, вони паралельні.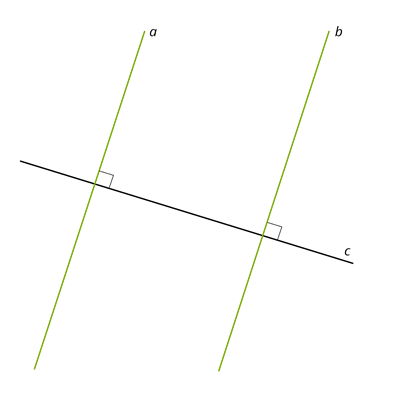 Цю ознаку легко довести, якщо згадати, що до прямої на площині з будь-якої точки можна провести лише один перпендикуляр.
Цю ознаку легко довести, якщо згадати, що до прямої на площині з будь-якої точки можна провести лише один перпендикуляр.
Припустимо, що прямі, перпендикулярні до однієї й тієї самої прямої, не є паралельними, тобто мають спільну точку.
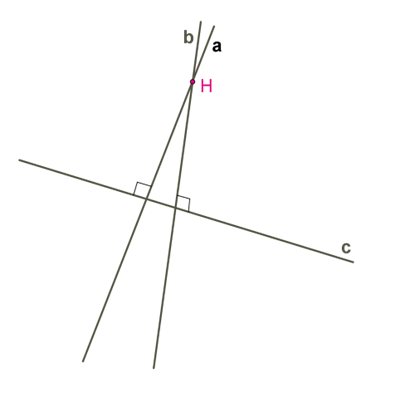 Виникає суперечність: із однієї точки
Виникає суперечність: із однієї точки H до прямої c проведено два перпендикуляри. Таке неможливо, тому дві прямі на площині, перпендикулярні до однієї й тієї самої прямої, є паралельними.Щоб розглянути інші ознаки, потрібно ознайомитися з деякими видами кутів1. Пригадаємо, які нам відомі назви та властивості кутів, утворених двома прямими, що перетинаються. 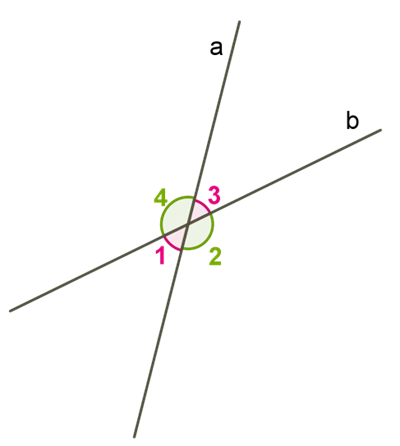
Вертикальні кути рівні: ∠1=∠3;∠2=∠4
Сума суміжних кутів складає 180° : ∠1+∠2=∠2+∠3=∠3+∠4=∠4+∠1=180° 2. Назви та властивості кутів, утворених при перетині двох прямих третьою (січною):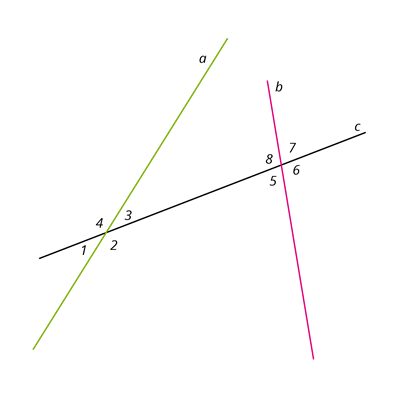 Нехай пряма
Нехай пряма c перетинає прямі a і b у двох різних точках. У такому разі кажуть, що пряма c є січною прямих a і b . У результаті такого перетину двох прямих третьою утворюються пари нерозгорнутих кутів, які мають спеціальні назви:- внутрішні різносторонні кути лежать між прямими
a і b по різні боки від січної: ∠3і∠5;∠2і∠8; - внутрішні односторонні кути лежать між прямими
a і b по один бік від січної: ∠3і∠8;∠2і∠5; - відповідні кути лежать по один бік від січної, причому сторона одного з них є частиною сторони другого:
∠1і∠5;∠4і∠8;∠2і∠6;∠3і∠7.
Ці кути допоможуть визначити паралельність прямих a і b. Доведемо ще кілька ознак паралельності прямих:Якщо при перетині двох прямих січною виконується принаймні одна з умов:
1) внутрішні різносторонні кути рівні;
2) сума внутрішніх односторонніх кутів дорівнює 180°;
3) відповідні кути рівні,
то дані прямі паралельні.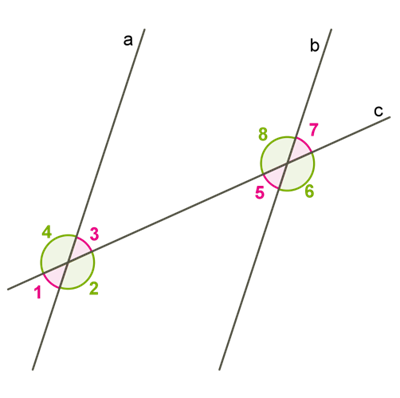 Доведемо цю ознаку. Якщо при перетині прямих
Доведемо цю ознаку. Якщо при перетині прямих a і b прямою c внутрішні різносторонні кути рівні, то прямі a і b паралельні. Наприклад, якщо ∠3=∠5 , то a∥b . 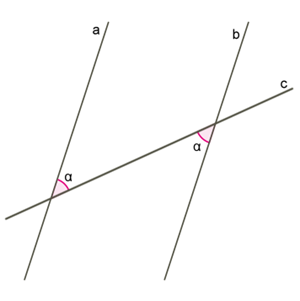
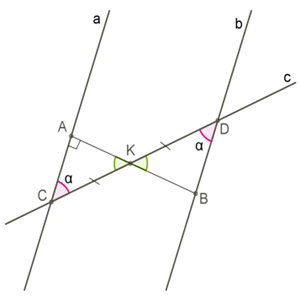
1. Позначимо точки C і D, у яких прямі a і b перетинає пряма c. Через середину відрізка CD точку K цього відрізка проведемо перпендикуляр AB до прямої a. 2. ∠CKA = ∠DKB як вертикальні кути, ∠3 = ∠5 = α , CK=KD, отже ΔCKA = ΔDKB за ознакою про сторону та два кути. 3. Зрозуміло, що якщо ΔCKA прямокутний, то й ΔDKB прямокутний, і AB перпендикулярний до прямої b.
4. Прямі, перпендикулярні до однієї й тієї самої прямої, є паралельними (відповідно до першої доведеної ознаки). 5. У випадку, коли відповідні кути рівні, маємо на увазі, що вертикальні кути рівні, і доводимо, як у пунктах 1–4. 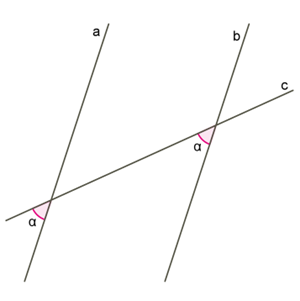
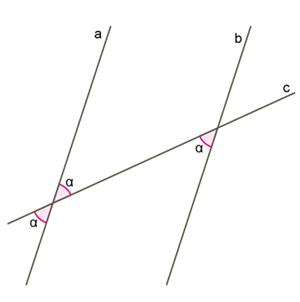
6. У випадку, коли сума внутрішніх односторонніх кутів дорівнює 180°, маємо на увазі, що сума суміжних кутів також дорівнює 180° і використовуємо в доведенні пункти 1–4. 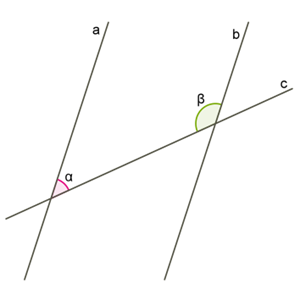
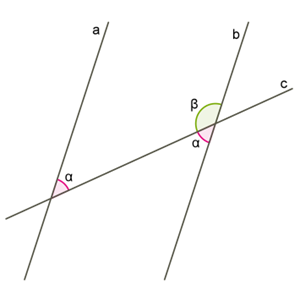 Ознака паралельних прямих діє і як властивість паралельних прямих.При перетині двох паралельних прямих третьою січною:
Ознака паралельних прямих діє і як властивість паралельних прямих.При перетині двох паралельних прямих третьою січною: - внутрішні різносторонні кути рівні;
- відповідні кути рівні;
- сума внутрішніх односторонніх кутів дорівнює
180° .


Через точку, що не лежить на даній прямій, можна провести пряму, паралельну даній, і до того ж тільки одну.




- внутрішні різносторонні кути лежать між прямими
a іb по різні боки від січної:∠3і∠5;∠2і∠8; - внутрішні односторонні кути лежать між прямими
a іb по один бік від січної:∠3і∠8;∠2і∠5; - відповідні кути лежать по один бік від січної, причому сторона одного з них є частиною сторони другого:
∠1і∠5;∠4і∠8;∠2і∠6;∠3і∠7.
то дані прямі паралельні.







- внутрішні різносторонні кути рівні;
- відповідні кути рівні;
- сума внутрішніх односторонніх кутів дорівнює
180° .
ві прямі, що перетинаються під прямим кутом, називаються перпендикулярними.  Скорочено це записують так:
Скорочено це записують так: a⊥b Відрізки або промені називаються перпендикулярними, якщо вони лежать на перпендикулярних прямих.Теорема (про дві прямі, перпендикулярні до третьої).Дві прямі, перпендикулярні до третьої, паралельні.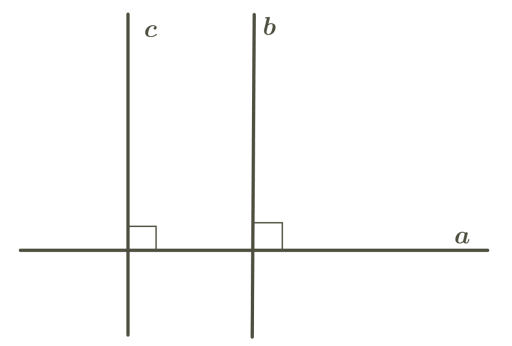 Твердження теореми ілюструє рисунок. На цьому рисунку
Твердження теореми ілюструє рисунок. На цьому рисунку a⊥b,a⊥c,b∥c. Ця властивість використовується для побудови паралельних прямих за допомогою лінійки та косинця. Двічі прикладаючи косинець до лінійки, можна провести дві прямі, перпендикулярні до краю лінійки.Теорема (про існування і єдиність перпендикулярної прямої)
Через будь-яку точку площини можна провести пряму, перпендикулярну до даної, і тільки одну.Зверни увагу!Теорема містить два твердження:
1) існує пряма, що проходить через дану точку площини і є перпендикулярною до даної прямої;
2) така пряма єдина.Перше твердження теореми говорить про існування прямої з описаними властивостями, друге — про її єдиність.
Перпендикуляром до даної прямої, проведеним із точки A, називається відрізок прямої, перпендикулярної до даної, одним із кінців якого є точка А, а другим (основою перпендикуляра) — точка перетину цих прямих.Відстанню від точки до прямої, яка не проходить через дану точку, називається довжина перпендикуляра, проведеного з даної точки до даної прямої.


Через будь-яку точку площини можна провести пряму, перпендикулярну до даної, і тільки одну.
Домашнє завдання : параграф 5,13 повторити, № 693 письмово
Завдання на період з 09.05 по 13.05 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 13.05
Тема : "Корекція знань,умінь та навичок.
Повторення теми :«Елементарні геометричні фігури та їх властивості»"

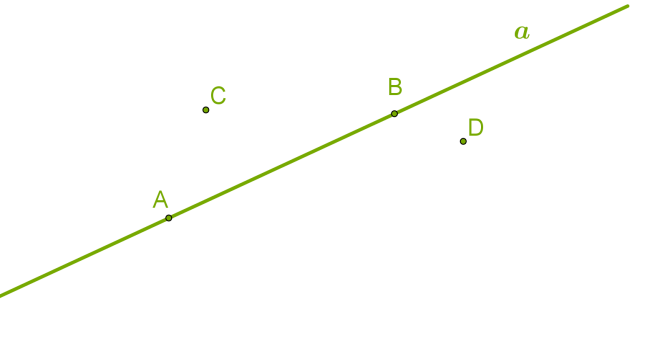
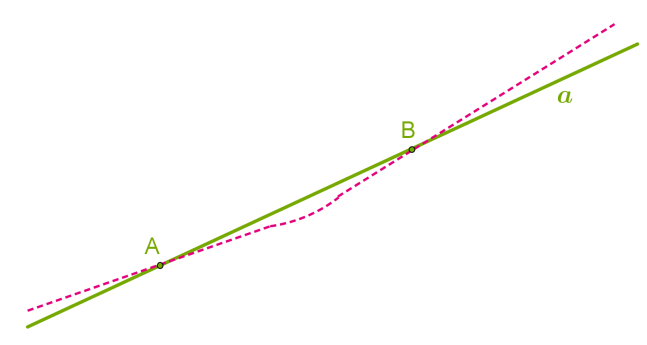
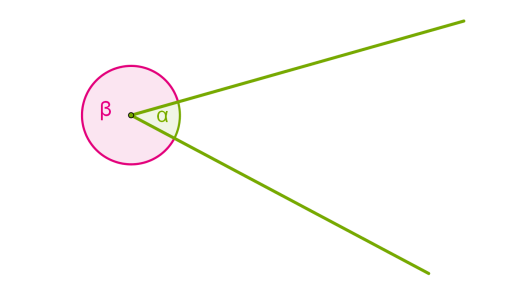
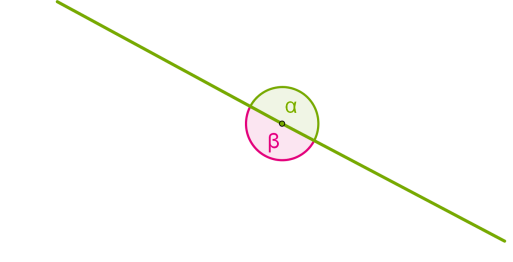
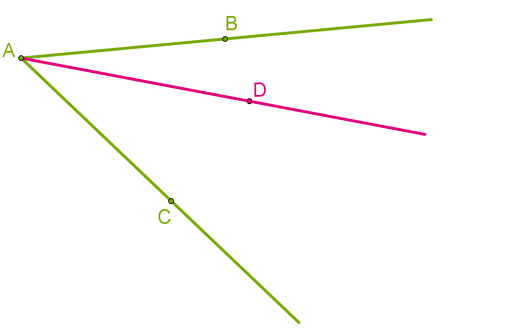
відрізки
Ми бачимо лише частини нескінченних прямих.
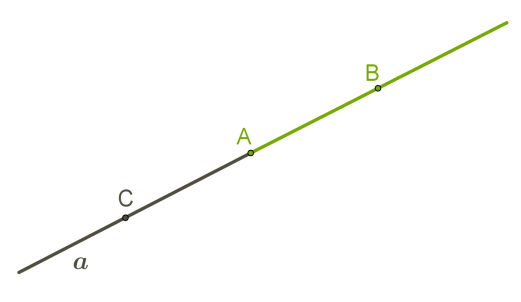
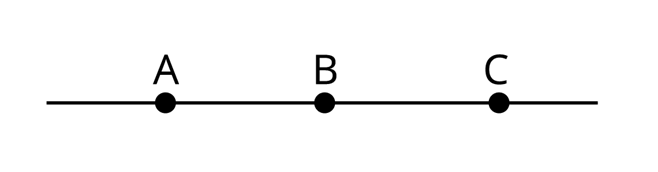
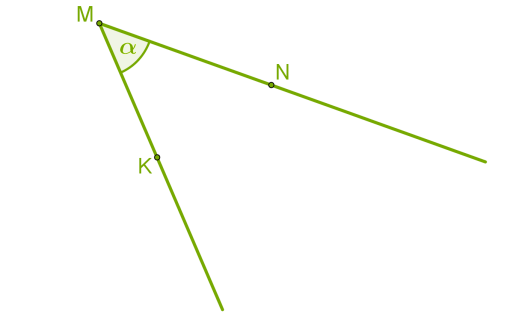
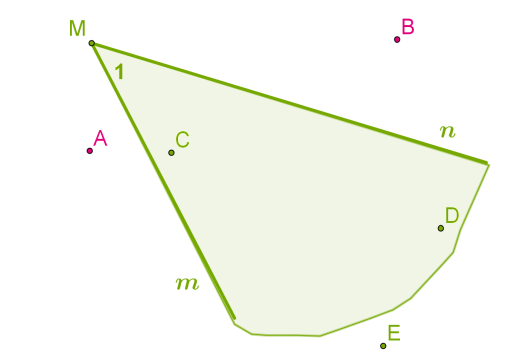
Домашнє завдання : параграф 1-6 повторити, № 669,672 письмово
Дата 10.05
Тема : "Контрольна робота з теми: «Коло і круг»."
Виконати контрольну роботу за посиланням :https://docs.google.com/document/d/1_2JN-i1bLgVpmZ6-vquwRxNtriIfXf-9/edit?usp=sharing&ouid=114690071356165548445&rtpof=true&sd=true
Домашнє завдання : параграф 19-23 повторити, виконати контрольну роботу
Завдання на період з 02.05 по 06.05 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 06.05
Тема : "Узагальнення та систематизація знань умінь і навичок учнів з теми: «Коло і круг»."
Переглянути відео :https://www.youtube.com/watch?v=a_NoM-Wopc8
Опрацювати матеріал :
Коло
Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки – центра кола.
Радіус кола – відстань від точок кола до його центра. Радіус кола зазвичай позначається буквами
Хорда
Хорда – відрізок, який з'єднує будь-які дві точки кола. Хорда, що проходить через центр кола, називається діаметром. Діаметр рівний подвоєному радіусу кола. Діаметр зазвичай позначають буквами , . Дотична – пряма, яка проходить через точку кола перпендикулярно до радіуса, проведеного в цю точку. Через будь-яку точку, що лежить поза колом і належить площині кола, можна провести дві різні дотичні. Пряма, що має з колом дві спільні точки, називається січною. Довжиною кола називається границя послідовності периметрів правильних багатокутників, які вписані в дане коло, при необмеженому збільшенні кількості сторін. Довжина кола обчислюється за формулою:
С = Пd або С =2 Пr
Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки – центра кола.
Радіус кола – відстань від точок кола до його центра. Радіус кола зазвичай позначається буквами
Хорда
Хорда – відрізок, який з'єднує будь-які дві точки кола. Хорда, що проходить через центр кола, називається діаметром. Діаметр рівний подвоєному радіусу кола. Діаметр зазвичай позначають буквами , . Дотична – пряма, яка проходить через точку кола перпендикулярно до радіуса, проведеного в цю точку. Через будь-яку точку, що лежить поза колом і належить площині кола, можна провести дві різні дотичні. Пряма, що має з колом дві спільні точки, називається січною. Довжиною кола називається границя послідовності периметрів правильних багатокутників, які вписані в дане коло, при необмеженому збільшенні кількості сторін. Довжина кола обчислюється за формулою:
С = Пd або С =2 Пr
Круг
Кругом називається фігура, яка складається з усіх точок площини, відстань від яких до даної точки не перевищує заданої. Ця точка – центр круга. Радіус – задана відстань. Радіус, хорда і діаметр кола є радіусом, хордою та діаметром відповідного кругу.
Коло описане навколо трикутника
Коло називається описаним навколо трикутника, якщо воно проходить через усі його вершини.
Теорема 3. Навколо будь-якого трикутника можна описати коло. Його центр — точка перетину серединних перпендикулярів до сторін трикутника. Зверніть увагу: у гострокутному трикутнику центр описаного кола лежить у середині трикутника (рисунок нижче зліва). У прямокутному трикутнику центр описаного кола — середина гіпотенузи (рисунок посередині). Центр кола, описаного навколо тупокутного трикутника, лежить поза трикутником
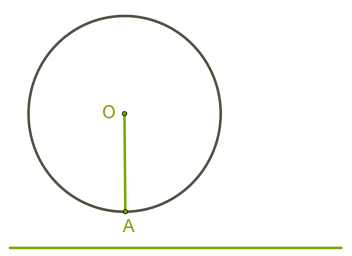
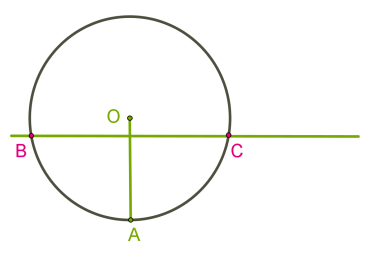
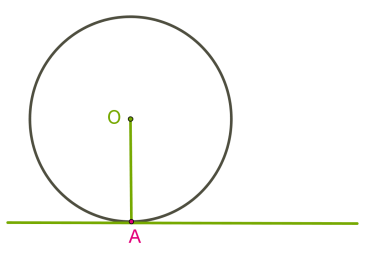
Дотична до кола
Пряма, що проходить через точку кола перпендикулярно до радіуса, проведеного в цю точку, називається дотичною. Дана точка кола називається точкою дотику. Теорема 1. Дотична до кола має з ним єдину спільну точку — точку дотику.
Коло вписане в трикутник
Коло називається вписаним у трикутник, якщо воно дотикається до всіх його сторін. Теорема 2. У будь-який трикутник можна вписати коло. Центр кола, вписаного в трикутник, є точкою перетину його бісектрис. Теорема 3. Із будь-якої точки поза колом можна провести до кола дві дотичні. Відрізки цих дотичних від даної точки до точок дотику рівні. Промінь, що виходить із даної точки й проходить крізь центр кола, є бісектрисою кута між дотичними. На рисунку нижче AB і AC — дотичні. Теорема стверджує, що AB = AC; AO — бісектриса .
Метод геометричних місць
Геометричним місцем точок (ГМТ), які мають певну властивість, називається така фігура, що складається з усіх точок площини, які мають цю властивість, і тільки з них. Довести, що фігура М є ГМТ, які мають властивість Р, означає довести два такі твердження. 1. Якщо точка А ∈ М, то вона має властивість Р. 2. Якщо точка А має властивість Р, то А є М. Приклади 1) Коло — це ГМТ, рівновіддалених від даної точки. 2) Бісектриса кута — це ГМТ, рівновіддалених від сторін кута
Кругом називається фігура, яка складається з усіх точок площини, відстань від яких до даної точки не перевищує заданої. Ця точка – центр круга. Радіус – задана відстань. Радіус, хорда і діаметр кола є радіусом, хордою та діаметром відповідного кругу.
Коло описане навколо трикутника
Коло називається описаним навколо трикутника, якщо воно проходить через усі його вершини.
Теорема 3. Навколо будь-якого трикутника можна описати коло. Його центр — точка перетину серединних перпендикулярів до сторін трикутника. Зверніть увагу: у гострокутному трикутнику центр описаного кола лежить у середині трикутника (рисунок нижче зліва). У прямокутному трикутнику центр описаного кола — середина гіпотенузи (рисунок посередині). Центр кола, описаного навколо тупокутного трикутника, лежить поза трикутником
Дотична до кола
Пряма, що проходить через точку кола перпендикулярно до радіуса, проведеного в цю точку, називається дотичною. Дана точка кола називається точкою дотику. Теорема 1. Дотична до кола має з ним єдину спільну точку — точку дотику.
Коло вписане в трикутник
Коло називається вписаним у трикутник, якщо воно дотикається до всіх його сторін. Теорема 2. У будь-який трикутник можна вписати коло. Центр кола, вписаного в трикутник, є точкою перетину його бісектрис. Теорема 3. Із будь-якої точки поза колом можна провести до кола дві дотичні. Відрізки цих дотичних від даної точки до точок дотику рівні. Промінь, що виходить із даної точки й проходить крізь центр кола, є бісектрисою кута між дотичними. На рисунку нижче AB і AC — дотичні. Теорема стверджує, що AB = AC; AO — бісектриса .
Метод геометричних місць
Геометричним місцем точок (ГМТ), які мають певну властивість, називається така фігура, що складається з усіх точок площини, які мають цю властивість, і тільки з них. Довести, що фігура М є ГМТ, які мають властивість Р, означає довести два такі твердження. 1. Якщо точка А ∈ М, то вона має властивість Р. 2. Якщо точка А має властивість Р, то А є М. Приклади 1) Коло — це ГМТ, рівновіддалених від даної точки. 2) Бісектриса кута — це ГМТ, рівновіддалених від сторін кута
Домашнє завдання : параграф 19-23 повторити, тести сторінка 193-194 письмово
Дата 03.05
Тема : "Розв’язування вправ."
Переглянути відео :https://www.youtube.com/watch?v=isYBP4WWj4w
Опрацювати матеріал :
Коло, вписане в трикутник
Коло називається вписаним у трикутник, якщо воно дотикається до всіх сторін трикутника. Сторони трикутника є дотичними до вписаного в нього кола.
У будь-який трикутник можна вписати коло і лише одне. Центр кола, вписаного в трикутник, є точкою перетину бісектрис трикутника.
Зверніть увагу! Щоб знайти центр уписаного кола, достатньо провести бісектриси двох кутів трикутника, оскільки всі три бісектриси трикутника перетинаються в одній точці.
Щоб вписати коло в трикутник, треба знайти центр кола й опустити з нього перпендикуляр на будь-яку сторону трикутника. Радіусом, що дорівнює довжині перпендикуляра, побудувати коло.
Діаметр кола, вписаного в прямокутний трикутник, дорівнює різниці суми катетів і гіпотенузи.
У рівностороннього трикутника центри вписаного й описаного кіл збігаються.
У рівнобедреного трикутника центри вписаного й описаного кіл лежать на медіані, проведеній до основи трикутника.
Це цікаво.
Слово «циркуль» з латини означає коло, круг, обвід. Це прилад для креслення кіл і їх дуг, для лінійних вимірювань і перенесення різних розмірів. Циркуль був відомий давно, ним користувались ще в Стародавньому Вавилоні й Ассирії. Старогрецькі математики циркуль поряд із лінійкою вважали основним приладом для виконання геометричних побудов. При цьому задачу вважали розв’язаною, якщо вона зводилась до побудов за допомогою циркуля і лінійки.
Є багато різновидів циркулів: циркулі із загнутими кінцями для вимірювання внутрішніх (нутромір) і зовнішніх (кронциркуль) діаметрів предметів, пропорціональні циркулі для збільшення або зменшення масштабів. Усі вони були відомі майже 2 тисячі років тому, крім пропорційного циркуля, винахід якого в 1607 році приписують Галілею.
Коло, вписане в трикутник
Коло називається вписаним у трикутник, якщо воно дотикається до всіх сторін трикутника. Сторони трикутника є дотичними до вписаного в нього кола.
У будь-який трикутник можна вписати коло і лише одне. Центр кола, вписаного в трикутник, є точкою перетину бісектрис трикутника.
Зверніть увагу! Щоб знайти центр уписаного кола, достатньо провести бісектриси двох кутів трикутника, оскільки всі три бісектриси трикутника перетинаються в одній точці.
Щоб вписати коло в трикутник, треба знайти центр кола й опустити з нього перпендикуляр на будь-яку сторону трикутника. Радіусом, що дорівнює довжині перпендикуляра, побудувати коло.
Діаметр кола, вписаного в прямокутний трикутник, дорівнює різниці суми катетів і гіпотенузи.
У рівностороннього трикутника центри вписаного й описаного кіл збігаються.
У рівнобедреного трикутника центри вписаного й описаного кіл лежать на медіані, проведеній до основи трикутника.
Це цікаво.
Слово «циркуль» з латини означає коло, круг, обвід. Це прилад для креслення кіл і їх дуг, для лінійних вимірювань і перенесення різних розмірів. Циркуль був відомий давно, ним користувались ще в Стародавньому Вавилоні й Ассирії. Старогрецькі математики циркуль поряд із лінійкою вважали основним приладом для виконання геометричних побудов. При цьому задачу вважали розв’язаною, якщо вона зводилась до побудов за допомогою циркуля і лінійки.
Є багато різновидів циркулів: циркулі із загнутими кінцями для вимірювання внутрішніх (нутромір) і зовнішніх (кронциркуль) діаметрів предметів, пропорціональні циркулі для збільшення або зменшення масштабів. Усі вони були відомі майже 2 тисячі років тому, крім пропорційного циркуля, винахід якого в 1607 році приписують Галілею.
Домашнє завдання : параграф 21 повторити, № 558
Завдання на період з 25.04 по 29.04 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 29.04
Тема : "Коло , вписане в трикутник"
Переглянути відео :https://www.youtube.com/watch?v=JBdNHDe-OPQ
Опрацювати матеріал :
Коло, вписане в трикутникКоло називається вписаним у трикутник, якщо всі сторони трикутника дотикаються до кола.Його центр рівновіддалений від усіх сторін, тобто повинен розміщуватися в точці перетину бісектрис трикутника. Отже, в будь-який трикутник можна вписати коло, оскільки бісектриси трикутника перетинаються в одній точці. 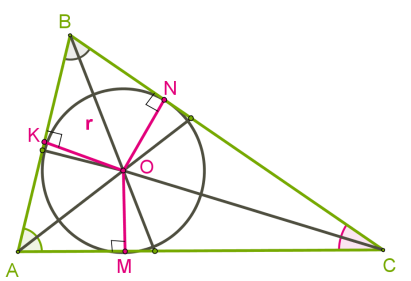 Оскільки бісектриси кутів трикутника завжди перетинаються всередині трикутника, то для всіх трикутників центр вписаного кола розташовується в трикутниках.Формули (рівносторонній трикутник)Зверни увагу!У рівностороннього трикутника збігаються бісектриси, медіани й висоти, тобто ці відрізки є також серединними перпендикулярами. Це означає, що центри вписаного та описаного кіл збігаються.Радіус описаного кола
Оскільки бісектриси кутів трикутника завжди перетинаються всередині трикутника, то для всіх трикутників центр вписаного кола розташовується в трикутниках.Формули (рівносторонній трикутник)Зверни увагу!У рівностороннього трикутника збігаються бісектриси, медіани й висоти, тобто ці відрізки є також серединними перпендикулярами. Це означає, що центри вписаного та описаного кіл збігаються.Радіус описаного кола R=23h , тому R=a3–√3 . Радіус вписаного кола r=13h , де h — висота трикутника.Якщо дано сторону трикутника a, тоді h=a3–√2 . Отже, r=a3–√6 . Формули (прямокутний трикутник)Радіус описаного кола R=12c , де c — гіпотенуза. Радіус вписаного кола r=SΔp , де p — півпериметр.Формули (довільний трикутник)Радіус описаного кола R=a⋅b⋅c4⋅SΔ R=a2sinα , де α — кут, протилежний стороні a. Якщо SΔ=abc4R,то R=abc4SΔ;якщо SΔ=p⋅r,то r=SΔp Радіус вписаного кола r=SΔp , де p — півпериметр.

Домашнє завдання : параграф 21, стр.167-169 опрацювати, № 541
Дата 26.04
Тема : "Коло , описане навколо трикутника"
Переглянути відео :https://www.youtube.com/watch?v=2SOO23PRwBo
Опрацювати матеріал :Коло, описане навколо трикутникаКоло називається описаним навколо трикутника, якщо всі вершини трикутника розміщені на колі.Центр кола рівновіддалений від усіх вершин, тобто повинен розташовуватися в точці перетину серединних перпендикулярів до сторін трикутника.
Навколо будь-якого трикутника можна описати коло, оскільки серединні перпендикуляри до сторін перетинаються в одній точці.
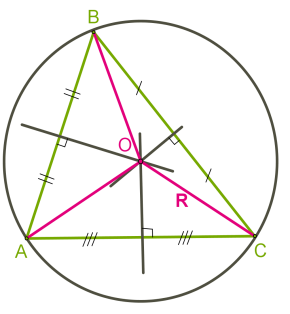
Для гострокутного трикутника центр кола знаходиться в трикутнику. Інша ситуація з прямокутним і тупокутним трикутниками.
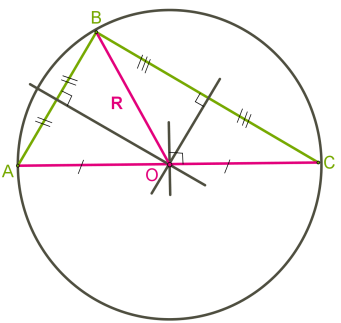
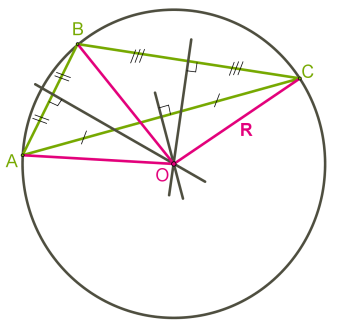



Домашнє завдання : параграф 21, стр.166-167 опрацювати, № 550,553
Завдання на період з 18.04 по 22.04 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 19.04
Тема : "Розв’язування вправ. Самостійна робота"
Переглянути відео :https://www.youtube.com/watch?v=916mGWajqfQ
Домашнє завдання : параграф 22,23 повторити,
Вказати правильну послідовність кроків при побудові циркулем і лінійкою бісектриси кута А.
А) Позначаємо точки В і С перетину кола із сторонами кута.
Б) Проводимо промінь АD.
В) Проводимо коло довільного радіуса з центром в точці А.
Г) Проводимо два кола з центрами в точках В і С однаковим радіусом.
Д) Позначаємо точку перетину кіл D.
Які інструменти використовують в задачах на побудову (декілька варіантів)?
На якому з рисунків зображено основні етапи побудови перпендикуляра до прямої через точку, що не лежить на даній прямій?
На якому з рисунків зображено основні етапи побудови середини заданого відрізка?
На якому з рисунків зображено основні етапи побудови бісектриси даного кута?
Чи можна за такою умовою виконати побудову:" Є відрізок АВ. За допомогою косинця і лінійки поділити його навпіл"?
Вказати правильні дії при поділі відрізка АВ навпіл циркулем та лінійкою.(декілька варіантів)
Визначне зайву дію у поділі відрізка АВ навпіл:
Визначне зайву дію при побудові бісектриси даного кута:
До основних геометричних побудов відносять: (декілька правильних)
Дата 19.04
Тема : "Побудова прямої ,перпендикулярної до даної"
Переглянути відео :https://www.youtube.com/watch?v=gR_1JI6IyvA
Опрацювати матеріал :
Побудова перпендикулярних прямих
Домашнє завдання : параграф 22,23 опрацювати, № 622
Завдання на період з 11.04 по 11.04 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 15.04
Тема : "Поділ даного відрізка навпіл"
Переглянути відео :https://www.youtube.com/watch?v=nR4Iw3qrH2Q
Опрацювати матеріал :
Ділення відрізків на рівні частини
Поділ відрізків на рівні частини. Багато предметів мають однакові елементи, рівномірно розташовані уздовж прямої. Тому виникає необхідність на кресленнях ділити відрізки прямих на рівні частини. Найпростіше це робити за допомогою лінійки з нанесеною на ній міліметровою шкалою. Але при такому поділі іноді виникають незручності. Нехай відрізок довжиною 47 мм потрібно поділити на 9 рівних частин або відрізок, що становить 19 мм, — на 2 частини. Як тут бути? Ось чому доцільніше застосовувати графічний метод — коли операція поділу виконується за допомогою циркуля і лінійки.
Поділ відрізка прямої на дві рівні частини. З обох кінців А і В заданого відрізка розхилом циркуля R, трохи більшим, ніж половина його довжини, описують дві дуги . Одержані у місцях перетину дуг точки С і D з'єднують між собою. Пряма, що з'єднала точки С і D, ділить відрізок АВ на дві рівні частини і перпендикулярна до нього.
Домашнє завдання : параграф 22 опрацювати, № 576
Дата 11.04
Тема : "Побудова кута , що дорівнює даному. Побудова бісектриси даного кута"
Переглянути відео :https://www.youtube.com/watch?v=bEfx96lp7YE
Опрацювати матеріал :
Побудова кута, що дорівнює даному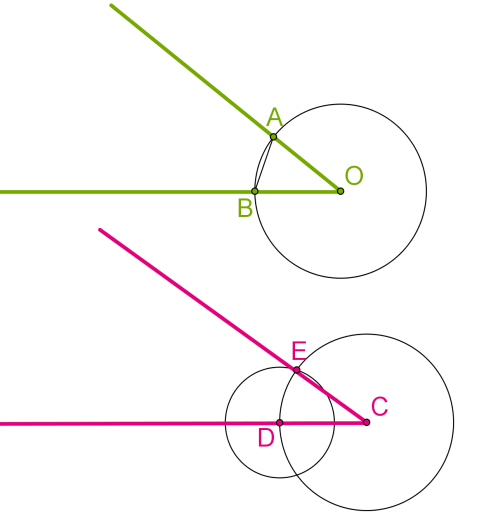
Доведемо, що побудований кут ECD і є той шуканий кут, що дорівнює даному куту AOB.
Якщо ми побудували коло з центром C (початковою точкою променя) і таким самим радіусом, як у кола з центром O, то CD = OB.
Якщо далі ми побудували коло з центром D і радісуом, рівним відрізку BA, і отримали точку перетину обох кіл E, то BA = DE.
Ми провели промінь CE. Очевидно, що OA = CE.
Отже, трикутники AOB і ECD рівні за третьою ознакою рівності трикутників. У рівних трикутників відповідні елементи рівні, зокрема кут ECD дорівнює куту AOB.
Побудова бісектриси кута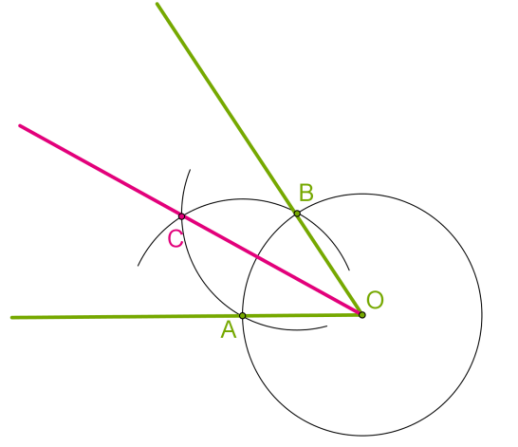 Щоб довести, що
Щоб довести, що OC дійсно ділить кут AOB навпіл, достатньо розглянути трикутники AOC і BOC.
OA=OB як радіуси одного кола, а AC=BC, оскільки при побудові ми вибрали однакові радіуси для обох кіл.
Сторона OC — спільна.
Ці трикутники рівні за третьою ознакою рівності трикутників, тож їх відповідні кути рівні.
Отже, AOC і BOC — дві рівні частини одного кута, і це означає, що промінь OC ділить кут навпіл.

Якщо ми побудували коло з центром
Якщо далі ми побудували коло з центром
Ми провели промінь
Отже, трикутники

Сторона
Ці трикутники рівні за третьою ознакою рівності трикутників, тож їх відповідні кути рівні.
Отже,
Домашнє завдання : параграф 22 опрацювати, № 575,577
Завдання на період з 04.04 по 08.04 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 08.04
Тема : "Основні задачі на побудову. Побудова трикутника за трьома сторонами"
Переглянути відео :https://www.youtube.com/watch?v=42XZ0IkammQ
Опрацювати матеріал :Побудова трикутника за трьома елементамиІснують такі основні задачі на побудову за допомогою циркуля та лінійки: 1. Як провести коло з даними центром і радіусом.
2. Як на даному промені від його початку відкласти відрізок, рівний даному.
3. Як побудувати кут, рівний даному.4. Як провести бісектрису кута.
5. Як побудувати перпендикулярну пряму.
6. Як прокласти середину відрізка. Використовуючи ці побудови й дані елементи трикутника, можна побудуватитрикутник, рівний даному.Приклад:Побудова трикутника за двома сторонами й кутом між нимиДано два відрізки a і b, які дорівнюють сторонам шуканого трикутника, і кут ∠ 1, що дорівнює куту трикутника між сторонами. Необхідно побудувати трикутник із елементами, що дорівнюють даним відрізкам і куту.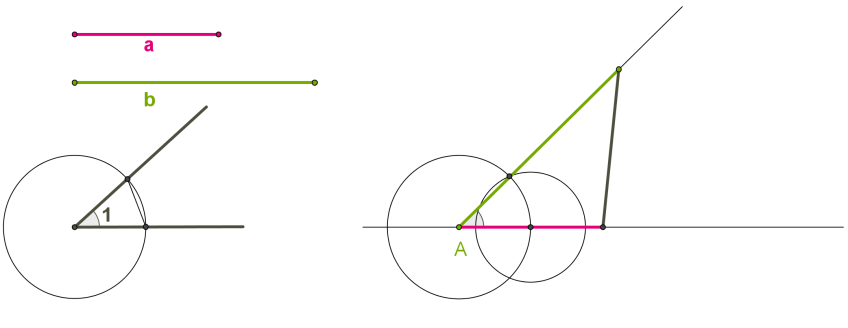 Кроки розв'язання
Кроки розв'язання1. Провести пряму.
2. На прямій від вибраної точки A відкласти відрізок, що дорівнює даному відрізку a.
3. Побудувати кут, що дорівнює даному ∠ 1 (вершина кута A, одна сторона кута лежить на прямій).
4. На іншій стороні кута відкласти відрізок, що дорівнює даному відрізку b.
5. З'єднати кінці відрізків.
Згідно з ознакою рівності трикутників за двома сторонами й кутом між ними, побудований трикутник дорівнює всім трикутникам, які мають дані елементи. Побудова трикутника за стороною і двома прилеглими до неї кутамиДано відрізок a і два кути ∠ 1 і ∠ 2, які дорівнюють кутам трикутника, прилеглим до даної сторони. Необхідно побудувати трикутник із елементами, які дорівнюють даному відрізку й кутам. 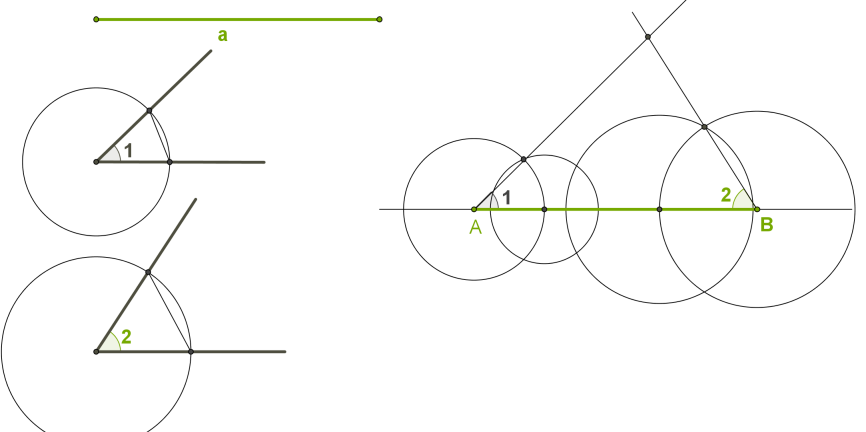 Кроки розв'язання
Кроки розв'язання1. Провести пряму.
2. На прямій від вибраної точки A відкласти відрізок, що дорівнює даному відрізку a, і позначити інший кінець відрізка B.
3. Побудувати кут, що дорівнює даному ∠ 1 (вершина кута A, одна сторона кута лежить на прямій).
4. Побудувати кут, що дорівнює даному ∠ 2 (вершина кута B, одна сторона кута лежить на прямій).
5. Точка перетину інших сторін кутів є третьою вершиною шуканого трикутника. Згідно з ознакою рівності трикутників за стороною та двома прилеглими до неї кутами, побудований трикутник дорівнює усім трикутникам, які мають дані елементи. Побудова трикутника за трьома сторонами
Дано три відрізки: a, b і c, що дорівнюють сторонам шуканого трикутника. Необхідно побудувати трикутник зі сторонами, що дорівнюють даним відрізкам. У цьому випадку перед початком побудови необхідно переконатися, чи виконується нерівність трикутника (довжина кожного відрізка менша від суми довжин двох інших відрізків), і ці відрізки можуть бути сторонами трикутника.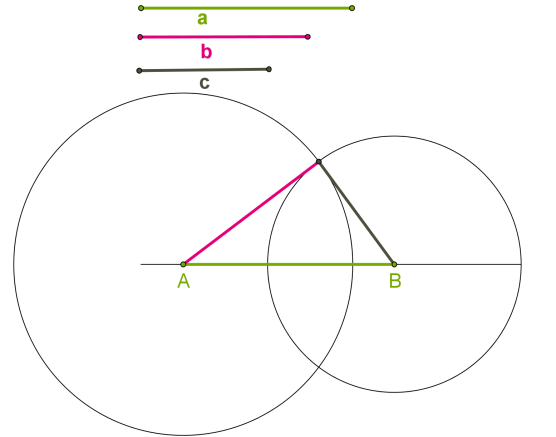 Якщо так, то виконати такі дії:
Якщо так, то виконати такі дії:1. Провести пряму.
2. На прямій від вибраної точки A відкласти відрізок, що дорівнює даному відрізку a, і позначити інший кінець відрізка B.
3. Провести коло з центром A і радіусом, що дорівнює відрізку b.
4. Провести коло з центром B і радіусом, що дорівнює відрізку c.
5. Точка перетину кіл є третьою вершиною шуканого трикутника. Згідно з ознакою рівності трикутників за трьома сторонами, побудований трикутник дорівнює всім трикутникам, які мають дані сторони.
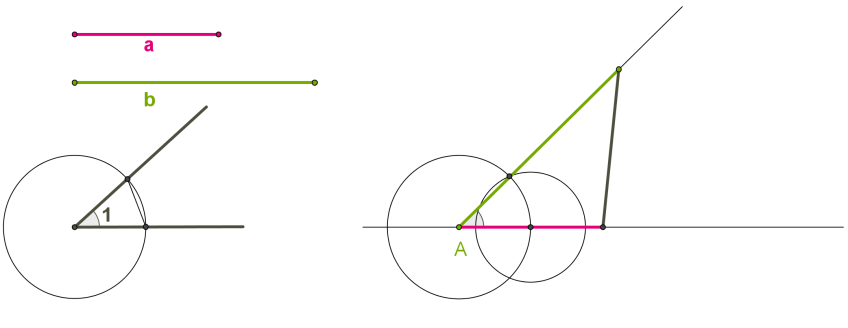
Згідно з ознакою рівності трикутників за двома сторонами й кутом між ними, побудований трикутник дорівнює всім трикутникам, які мають дані елементи.

Дано три відрізки:

Домашнє завдання : параграф 22 опрацювати ,№ 1-7 (Які знаходяться нижче)
Задачі на побудову трикутника за трьома сторонами розв'язують за допомогою:
За допомогою якого приладу вимірюють довжину відрізка при розв'язуванні задач на побудову?

Визначте кількість різних трикутників, які можна побудувати за заданими трьома сторонами: a= 4см, b=3 см, с=8 см.
*вказівка: пригадайте нерівність трикутника
Чи використовують лінійку при побудові трикутника за трьома сторонами для вимірювання точних відстаней?
Яку фігуру будують як допоміжну для знаходження третьої точки трикутника при розв'язуванні задач на побудову?
Яким є алгоритм побудови рівнобедреного трикутника за основою та бічною стороною?
1)проводимо два кола з центрами в кінцях відрізка заданої довжини
2)визначаємо точку перетину кіл
3)будуємо основу
4)з'єднуємо сторони трикутника
Чи можна побудувати рівносторонній трикутник, у якому дано довжину лише однієї сторони?
Пригадайте означення рівностороннього трикутника.
Дата 05.04
Тема : "Дотична до кола, її властивості"
Переглянути відео :https://www.youtube.com/watch?v=oYZFA11GGH4&ab_channel=%D0%A2%D0%BE%D0%BF%D0%A8%D0%BA%D0%BE%D0%BB%D0%B0
Опрацювати матеріал :
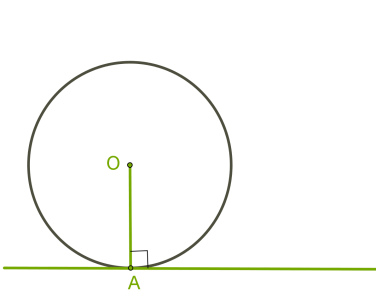
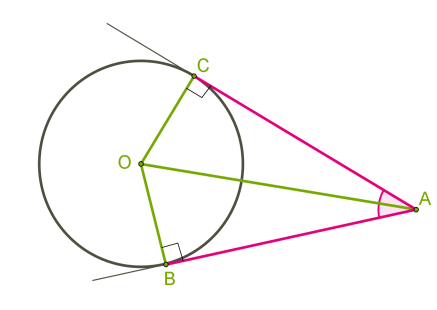
Домашнє завдання :параграф 20 опрацювати ,№ 509, 516
Завдання на період з 28.03 по 01.04 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 01.04
Тема : "Коло,круг"
Переглянути відео :https://www.youtube.com/watch?v=J4zEQ94fd2Y
Переглянути презентацію :https://docs.google.com/presentation/d/1yluCD3dINEcR9V3AZVpTq8ARzkDnEYKO/edit?usp=sharing&ouid=114690071356165548445&rtpof=true&sd=true
Теорія:

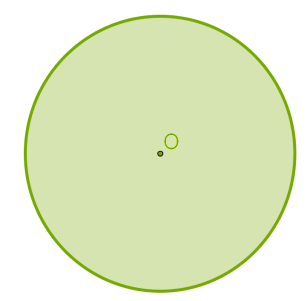 Коло — це фігура на площині, в якій усі точки розташовані на рівній відстані від однієї точки , яка є центром кола. Відстань від центра кола до будь - якої точки кола називається радіусом і в записах позначається буквою R. Радіус — з латинського слова radius - " спиця в колесі".
Коло — це фігура на площині, в якій усі точки розташовані на рівній відстані від однієї точки , яка є центром кола. Відстань від центра кола до будь - якої точки кола називається радіусом і в записах позначається буквою R. Радіус — з латинського слова radius - " спиця в колесі".
Центр кола найчастіше позначається буквою O. Коло ділить площину на дві частини: внутрішню та зовнішню.Внутрішня частина кола, що включає саме коло, називається кругом.Точка O — центр і кола, і круга.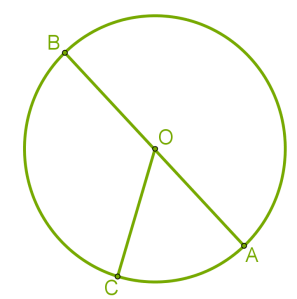
Відрізки OA, OB, OC — це радіуси, їх довжини рівні.Відрізок AB, що проходить через центр кола (круга), називається діаметром і позначається буквою D. Хорда — відрізок АВ , що з'єднує будь - які дві точки кола. 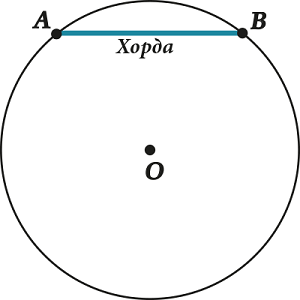 Діаметр кола — це найбільша хорда.
Діаметр кола — це найбільша хорда.
Довжина діаметра дорівнює довжині двох радіусів: D= 2R .Діаметр ділить коло на два півкола, а круг — на два півкруги. Точки на колі ділять коло на частини, які називаються дугами, а точки — кінцями цих дуг.На малюнку ми бачимо декілька дуг. Порахуй, скільки! Однією з них є дуга AB. 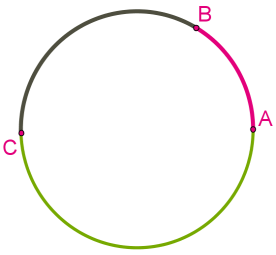

 Коло можна побудувати за допомогою циркуля.
Коло можна побудувати за допомогою циркуля.



Відрізки OA, OB, OC — це радіуси, їх довжини рівні.

Довжина діаметра дорівнює довжині двох радіусів: D



Домашнє завдання :параграф 19 опрацювати ,№ 484, 486
Дата 29.03
Тема : "Корекція знань ,умінь і навичок"
Переглянути відео :https://www.youtube.com/watch?v=_vwdFmbDX-w&t=2s&ab_channel=MONUKRAINE
Домашнє завдання :параграф 8,11,17, 18 повторити ,
№ 1
Завдання на період з 21.03 по 25.03 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 24.03
Тема : "Контрольна робота з теми "Ознаки рівності трикутників"
Домашнє завдання :параграф 8,11,17, 18 повторити
Дата 22.03
Тема : "Узагальнення та систематизація знань,умінь і навичок учнів з теми "Ознаки рівності трикутників"
Переглянути відео :https://www.youtube.com/watch?v=fn2FF-pbC8U&ab_channel=%D0%A2%D0%BE%D0%BF%D0%A8%D0%BA%D0%BE%D0%BB%D0%B0
Домашнє завдання :параграф 8,11,17, 18 повторити , № сторінка 97-99 тести
Завдання на період з 14.03 по 18.03 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 18.03
Тема : "Розвязування вправ"
Опрацювати матеріал : https://www.youtube.com/watch?v=G5fryaf--ig&t=629s
Сума гострих кутів прямокутного трикутника дорівнює 90°.
Якщо у прямокутному трикутнику один з гострих кутів дорівнює 30°, то протилежний цьому куту катет буде дорівнювати половині гіпотенузи.
Якщо катет прямокутного трикутника дорівнює половині гіпотенузи, то кут, що лежить проти цього катета, дорівнює 30°.
Домашнє завдання :параграф 17, 18 повторити ,номери 459,461
Дата 15.03
Тема : "Властивості прямокутних трикутників"
Опрацювати матеріал :https://www.youtube.com/watch?v=0UM2NvAWPPM
Властивості прямокутного трикутника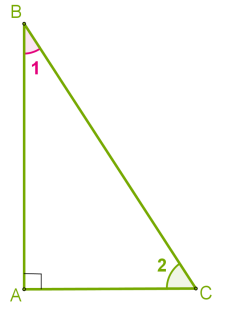 Прямокутний трикутник має один прямий і два гострі кути.Сторона прямокутного трикутника, протилежна прямому куту, називається гіпотенузою, дві інші сторони — катетами.На рисунку у трикутнику
Прямокутний трикутник має один прямий і два гострі кути.Сторона прямокутного трикутника, протилежна прямому куту, називається гіпотенузою, дві інші сторони — катетами.На рисунку у трикутнику △ ABC: ∠ А=90°, BC — гіпотенуза, AC і AB — катети.
З теореми про суму кутів трикутника випливає:сума гострих кутів прямокутного трикутника дорівнює 90°. Справедливе також обернене твердження, що є ознакою прямокутного трикутника:якщо в трикутнику сума двох кутів дорівнює 90°, то цей трикутник прямокутний.∠ 1+ ∠ 2= 90° .
Ознаки рівності прямокутних трикутниківКористуючись ознаками рівності трикутників і теоремою про суму кутів трикутника, можна сформулювати ознаки рівності характерні тільки для прямокутних трикутників:1. Ознака рівності прямокутних трикутників за двома катетами
Якщо два катети одного прямокутного трикутника відповідно дорівнюють двом катетам другого прямокутного
трикутника, то такі трикутники рівні.2. Ознака рівності прямокутних трикутників за катетом і прилеглим гострим кутом
Якщо катет і прилеглий до нього гострий кут одного прямокутного трикутника відповідно дорівнюють катету
й прилеглому до нього гострому куту другого прямокутного трикутника, то такі трикутники рівні.3. Ознака рівності прямокутних трикутників за катетом і протилежним кутом
Якщо катет і протилежний йому кут одного прямокутного трикутника відповідно дорівнюють катету й протилежному йому куту другого прямокутного трикутника, то такі трикутники рівні.4. Ознака рівності прямокутних трикутників за гіпотенузою й гострим кутом
Якщо гіпотенуза й гострий кут одного прямокутного трикутника відповідно дорівнюють гіпотенузі й гострому
куту другого прямокутного трикутника, то такі трикутники рівні.5. Ознака рівності прямокутних трикутників за гіпотенузою й катетом
Якщо гіпотенуза й катет одного прямокутного трикутника відповідно дорівнюють гіпотенузі й катету другого
прямокутного трикутника, то такі трикутники рівні.Прямокутний трикутник із кутом 30° Катет прямокутного трикутника, що лежить навпроти кута 30° , дорівнює половині гіпотенузи (гіпотенуза удвічі довша від катета навпроти кута 30° ).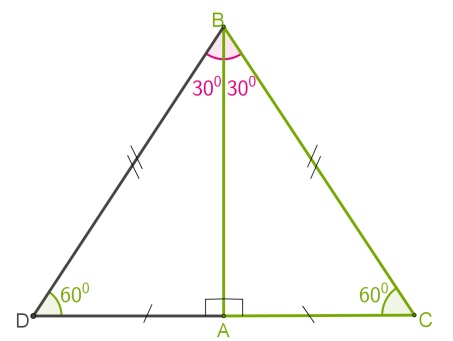 Розглянемо прямокутний трикутник
Розглянемо прямокутний трикутник ABC, у якому: ∠ A — прямий, ∠ B= 30° , отже ∠ C= 60° . Доведемо, що BC=2AC.
1. Прикладемо до трикутника △ ABC рівний йому трикутник △ ABD, як показано на рисунку. У них: ∠ C= ∠ D= 60° , як відповідні кути рівних трикутників. AD=AC, як відповідні сторони рівних трикутників.
2. Отримаємо трикутник △ BCD, у якому: ∠ C= ∠ D= 60° , то ∠ B= 60° , за теоремою про суму кутів трикутника. 3. Проти рівних кутів лежать рівні сторони. Звідси BC=DC=BD. Але DC=2AC. Отже, BC=DC=2AC. Правильним є і обернене твердження:Якщо катет прямокутного трикутника дорівнює половині гіпотенузи (або гіпотенуза удвічі довша від катета), то кут, що лежить навпроти цього катета, дорівнює 30° .

Якщо два катети одного прямокутного трикутника відповідно дорівнюють двом катетам другого прямокутного
трикутника, то такі трикутники рівні.
Якщо катет і прилеглий до нього гострий кут одного прямокутного трикутника відповідно дорівнюють катету
й прилеглому до нього гострому куту другого прямокутного трикутника, то такі трикутники рівні.
Якщо катет і протилежний йому кут одного прямокутного трикутника відповідно дорівнюють катету й протилежному йому куту другого прямокутного трикутника, то такі трикутники рівні.
Якщо гіпотенуза й гострий кут одного прямокутного трикутника відповідно дорівнюють гіпотенузі й гострому
куту другого прямокутного трикутника, то такі трикутники рівні.
Якщо гіпотенуза й катет одного прямокутного трикутника відповідно дорівнюють гіпотенузі й катету другого
прямокутного трикутника, то такі трикутники рівні.

Домашнє завдання :параграф 17, 18 опрацювати ,номери 427,430
Завдання на період з 24.02 по 25.02 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 25.02
Тема : "Розвязування вправ.Самостійна робота"
Опрацювати матеріал :https://www.youtube.com/watch?v=lMPQT_0jIbE
Всі ознаки рівності трикутників: 1. Якщо дві сторони і кут між ними одного трикутника відповідно дорівнюють двом сторонам і куту між ними іншого трикутника, то такі трикутники рівні.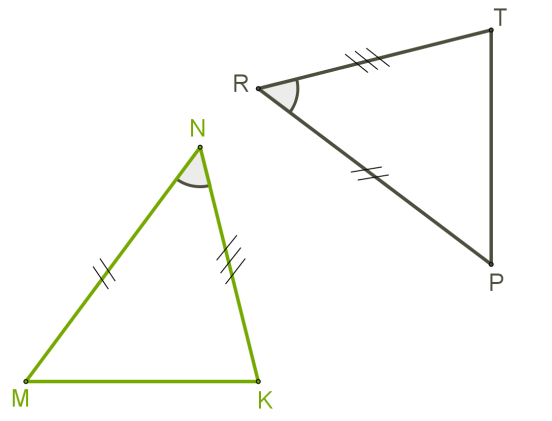 MN=PRKN=TR∠N=∠R
MN=PRKN=TR∠N=∠R
2. Якщо сторона і два прилеглі до неї кути одного трикутника відповідно дорівнюють стороні та двом прилеглим до неї кутам іншого трикутника, то такі трикутники рівні.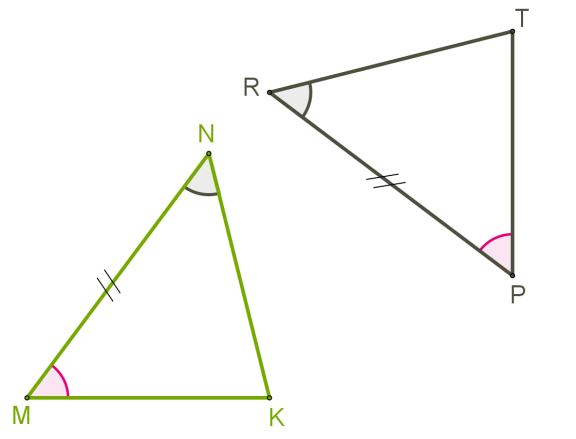
MN=PRKN=TR∠N=∠R
3. Якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам іншого трикутника, то такі трикутники рівні.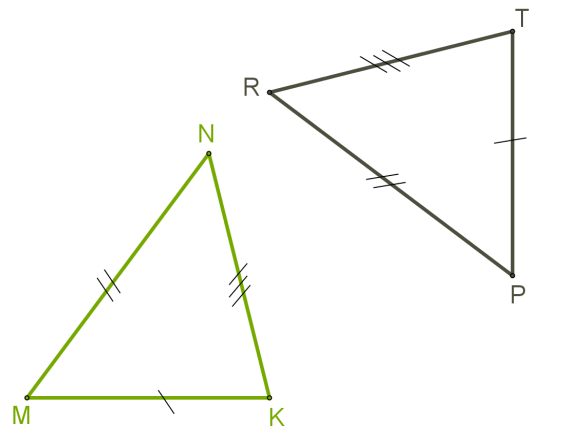
MN=PRKN=TR



MN=PRKN=TR
Домашнє завдання :параграф 8, 11 повторити , Виконати самостійну роботу за посиланням : https://docs.google.com/document/d/101bv0AaQ8gR2NaIccsLM9ExjXIlmkeKH/edit?usp=sharing&ouid=114690071356165548445&rtpof=true&sd=true
Завдання на період з 11.10 по 13.10
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 12.10 Тема : "Розвязування вправ"
Опрацювати матеріал :https://www.youtube.com/watch?v=QXG2caQkqSU
Суміжні та вертикальні кути, їх властивості
Суміжними називаються два кути, одна сторона яких спільна, а дві інші утворюють пряму, тобто є доповняльними променями.
Сума суміжних кутів дорівнює 180 градусам.
Два суміжних кути утворюють розгорнутий кут.
Якщо два кути рівні, то суміжні з ними кути теж рівні.
Кут, суміжний із прямим кутом, є прямим.
Кут, суміжний з гострим кутом, є тупим.
Кут, суміжний з тупим кутом, є гострим.
Будь-який промінь, що виходить із вершини розгорнутого кута і проходить між його сторонами, поділяє його на два суміжні кути.
Якщо два кути рівні, то суміжні з ними кути також рівні.
Два кути, суміжні з одним і тим же кутом, рівні.
Якщо два суміжні кути рівні, то вони прямі.
Вертикальними називаються два кути, сторони одного з яких є додатковими променями до сторін другого кута.
Вертикальні кути рівні.
При перетині двох прямих утворюються дві пари вертикальних кутів і чотири пари суміжних кутів.
Якщо відомий один із кутів, що утворились при перетині двох прямих, то знайти інші кути можна таким чином: знайти кут, суміжний з даним, враховуючи, що їх сума 180 градусів, після чого знайти кути, вертикальні з відомими, враховуючи, що вертикальні кути рівні.
Запам’ятайте поняття про теорему, аксіому та доведення.
Доведення — міркування про правильність твердження про властивість тієї або іншої геометричної фігури.
Теорема — твердження, яке треба довести.
Аксіома — твердження, що не потребують доведення, і які містяться у формулюваннях основних властивостей найпростіших фігур.
Домашнє завдання :параграф 4 повторити , № 104,107
Завдання на період з 04.10 по 08.10
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 08.10 Тема : "Вертикальні кути їх властивості"
Опрацювати матеріал :https://www.youtube.com/watch?v=8aNbmxcYGRs
Два кути називаються вертикальними, якщо обидві сторони одного кута є продовженням сторін другого.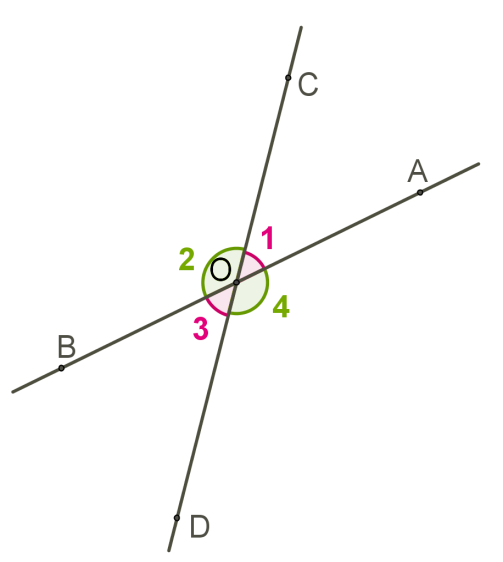 Якщо перетинаються дві прямі, то утворюються дві пари вертикальних кутів:
Якщо перетинаються дві прямі, то утворюються дві пари вертикальних кутів:∠1,∠3 і ∠2,∠4 . За властивістю суміжних кутів ∠1+∠2=180° і ∠1+∠4=180° . Отже,∠2=∠4 . Також зрозуміло, що ∠1=∠3 . Вертикальні кути рівні.Якщо один із вертикальних кутів прямий, тобто дорівнює 90° , то інші кути також прямі.Кутом між двома прямими, що перетинаються, називається менший із кутів, що утворилися в результаті перетину цих прямих.
∠ COB - кут між прямими СВ і АВ .


Домашнє завдання :параграф 4 стр.37 опрацювати , № 102
Дата 05.10 Тема : "Суміжні кути, їх властивості"
Опрацювати матеріал :https://www.youtube.com/watch?v=8ndT4U_c0lo
Два кути, у яких одна сторона спільна, а дві інші сторони є доповняльними променями, називаються суміжними.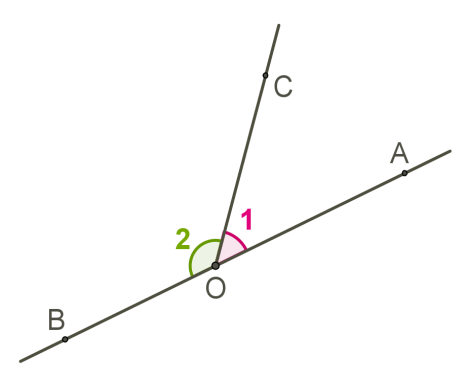 Оскільки
Оскільки ∠AOB=180° — розгорнутий кут і промінь OC ділить його на дві частини, то∠1+∠2=180° . Сума суміжних кутів дорівнює 180° .Зверни увагу!Властивості суміжних кутів- Якщо два кути рівні, то суміжні з ними кути також рівні.
- Два кути, суміжні з одним і тим самим кутом, рівні.
- Кут, суміжний і з прямим кутом, також прямий. Кут, суміжний із тупим кутом, гострий. Кут, суміжний із гострим кутом, тупий.

- Якщо два кути рівні, то суміжні з ними кути також рівні.
- Два кути, суміжні з одним і тим самим кутом, рівні.
- Кут, суміжний і з прямим кутом, також прямий. Кут, суміжний із тупим кутом, гострий. Кут, суміжний із гострим кутом, тупий.
Домашнє завдання :параграф 4 стр.36 опрацювати, № 95,98
Завдання на період з 27.09 по 01.10
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 01.10 Тема : "Корекція знань,умінь та навичок"
Опрацювати матеріал :
Назва нового предмету — «геометрія» — бере початок від давньогрецьких слів «земля» та «вимірюю» і в перекладі з грецької означає «землемірство». Геометрія є однією з найдавніших наук. Вона виникла у зв'язку з практичною необхідністю у вимірах, завдяки відновленню меж земельних ділянок, будівництву доріг та споруд. Нині ми знаємо геометрію як науку, що вивчає властивості геометричних фігур. Основними геометричними фігурами є точка і пряма, які можна уявити: точку — як найпростішу нескінченно малу фігуру, уявлення про яку можна отримати, якщо на аркуш паперу натиснути добре загостреним олівцем або на шкільну дошку — добре загостреним шматком крейди, а пряму — як нескінченну тонку натягнуту нитку, яка тягнеться безмежно в обидві сторони. За допомогою цих основних геометричних фігур можна визначити всі інші фігури. 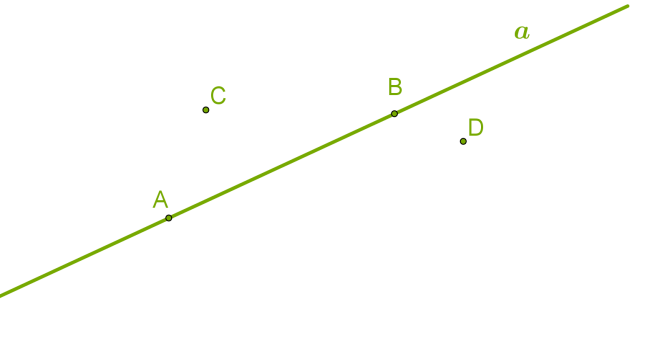 Точки позначаються великими латинськими буквами, а прямі — маленькими. Словесно описати взаємне розташування точок і прямої можна по-різному:
Точки позначаються великими латинськими буквами, а прямі — маленькими. Словесно описати взаємне розташування точок і прямої можна по-різному: 1. Точка розташована (лежить) на прямій, або пряма проходить (проведена) через точку.
2. Точка не розташована (не лежить) на прямій, або пряма не проходить (не проведена) через точку. У геометрії ці факти записуються символічно: 1. Точки A і B розташовані (лежать) на прямій a , або пряма a проходить (проведена) через точки A і B : A∈aі B∈a 2. Точки C і D не розташовані (не лежать) на прямій a , або пряма a не проходить (не проведена) через точки C і D : C∉aі D∉a Одна з найважливіших аксіом у геометрії:Через будь-які дві точки можна провести пряму, і до того ж тільки одну.Отже, іноді позначити пряму можна і двома великими латинськими буквами, наприклад пряма AB, оскільки жодна інша пряма через ці дві точки не може бути проведена. 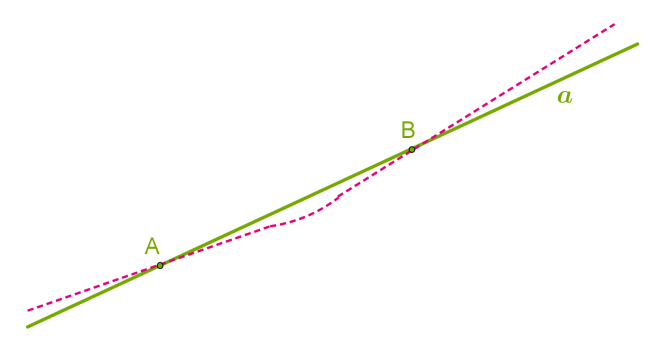 Отже, дві різні прямі можуть мати лише одну спільну точку й перетинатися або не мати жодної спільної точки і ніколи не перетинатися.
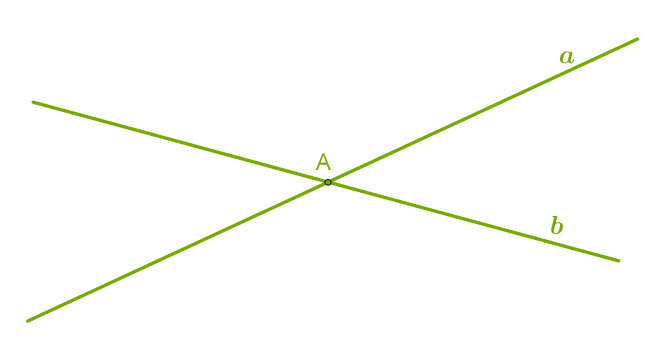
Отже, дві різні прямі можуть мати лише одну спільну точку й перетинатися або не мати жодної спільної точки і ніколи не перетинатися. 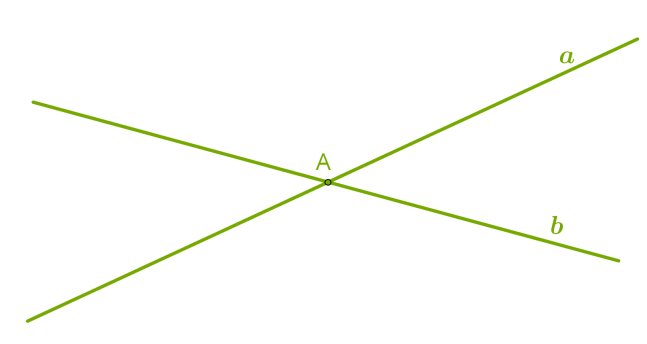 Символічно записуємо:
Символічно записуємо: a∩b=A 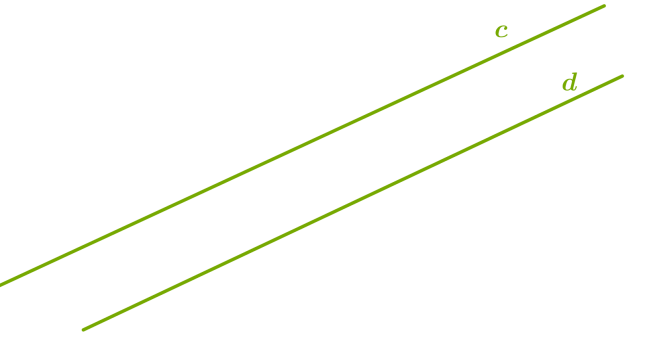 Символічно записуємо:
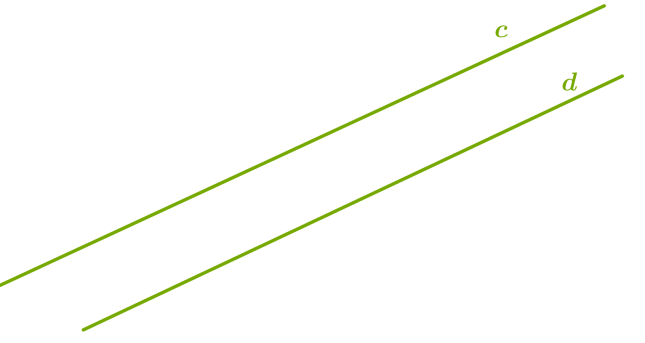
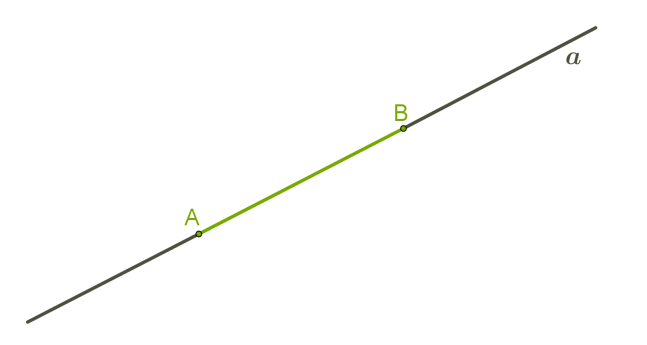
Символічно записуємо: c∥d Частина прямої, що складається з двох даних точок цієї прямої й усіх точок, що лежать між ними, називається відрізком. 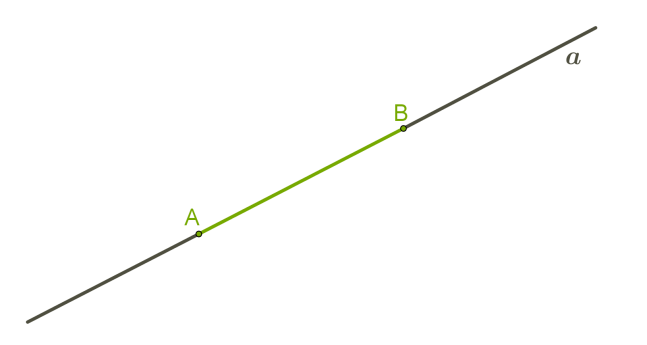 Символічно записуємо: відрізок
Символічно записуємо: відрізок AB Уважно подивися на рисунок!
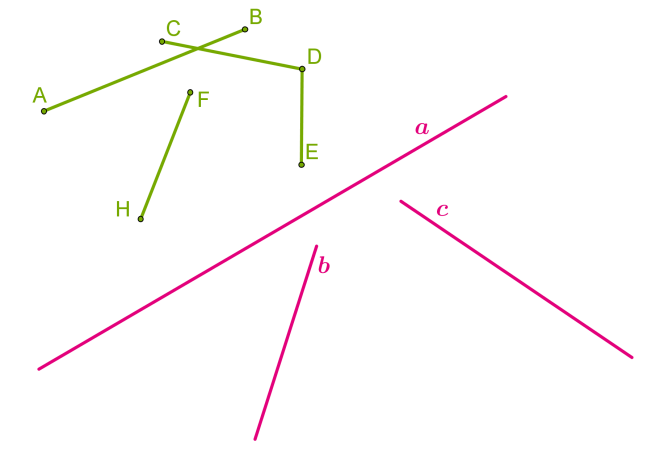 Зверни увагу!
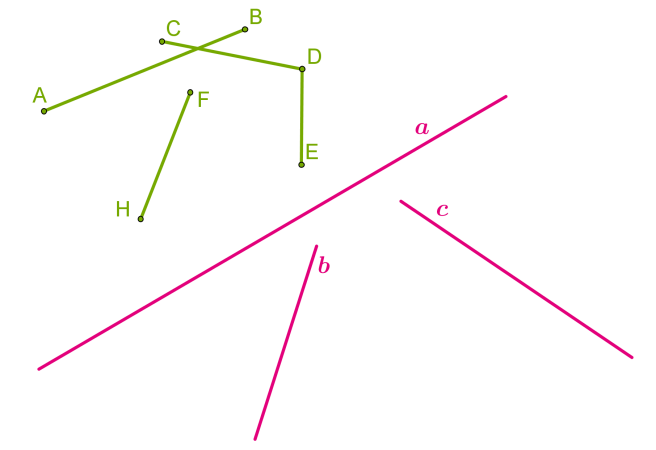
Зверни увагу! 1. Відрізки AB і CD перетинаються, відрізки CD і DE мають спільну точку,
відрізки AB і HF, AB і DE, CD і HF, HF і DE не перетинаються.
2. Прямі a, b і c перетинаються. Оскільки ми уявляємо пряму як нескінченну, що простягається в обидва боки, рано чи пізно ці прямі перетнуться (попри те, що на малюнку цього не видно).
Ми бачимо лише частини нескінченних прямихТочка, що лежить на прямій, ділить пряму на дві частини, кожна з яких називається променем, що виходить із цієї точки. Цю точку називають початком кожного з променів. 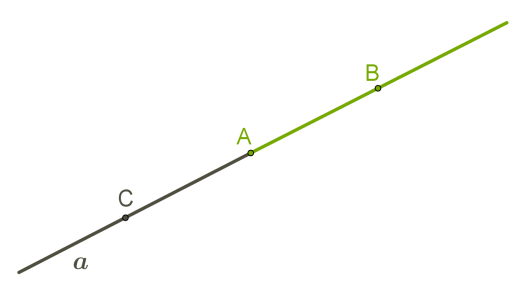 Точка
Точка A ділить пряму a на два промені. Оскільки важливо розуміти, який із променів розглядаємо, поставимо на прямій іще дві точки: B і C . Назвемо промені: промінь AB і промінь AC . Зверни увагу!Першою завжди називають початкову точку променя.На цьому рисунку кожна з точок може бути початковою точкою певного зображеного променя. З кожної точки виходять два промені в протилежні напрямки і, подібно до прямої, продовжуються нескінченно. Зверни увагу!Промінь BC — той самий промінь AC, але промінь BC відрізняється від променя AC. Ці промені мають певну спільну частину.Два різні промені однієї прямої зі спільною початковою точкою називаються доповняльними променями.ВА та ВС — доповняльні промені з початком у точці В . 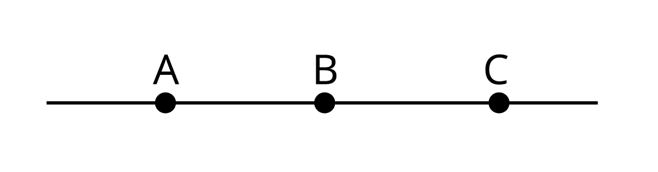 Зверни увагу!Об'єднавши промені
Зверни увагу!Об'єднавши промені СА та АС, ми також отримаємо пряму АС. Проте ці промені не є доповняльними: у них немає спільного початку.Кут — геометрична фігура, яка складається з точки і двох променів, що виходять із цієї точки. Ці промені називають сторонами кута, а їхній спільний початок — вершиною кута. 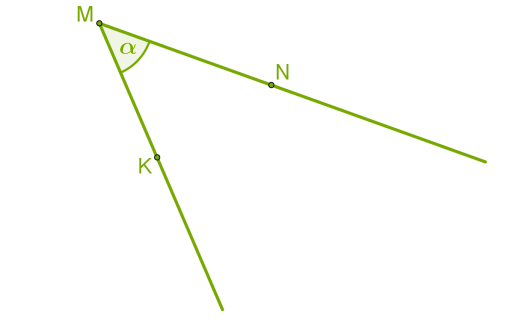 Кут позначають великими латинськими буквами, наприклад,
Кут позначають великими латинськими буквами, наприклад, ∠KMN , або малими грецькими буквами, наприклад, α . Зверни увагу!Кут ∠KMN можна назвати також ∠NMK , але буква, що позначає вершину, завжди пишеться посередині.Іноді кут можна позначити тільки однією великою латинською буквою вершини, цифрою або назвами променів — малими латинськими буквами, наприклад, ∠M , ∠1 або ∠mn . 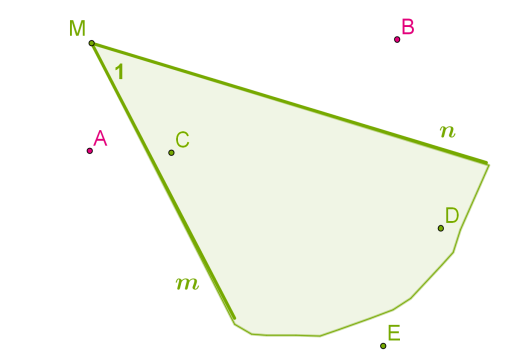 Промені
Промені n і m зі спільним початком у точці M ділять площину на дві частини: внутрішню і зовнішню область кута.
Кутом також можна називати промені зі спільним початком разом із внутрішньою областю. Тоді точки A і B не належать куту ∠M , а точки C, D і E належать куту ∠M . Якщо провести два промені, що виходять із однієї точки, то внутрішня область утворює один кут, а зовнішня область — інший. 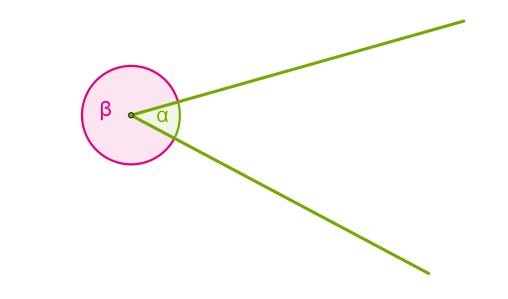 Якщо обидві сторони кута лежать на одній прямій, кут називається розгорнутим.
Якщо обидві сторони кута лежать на одній прямій, кут називається розгорнутим.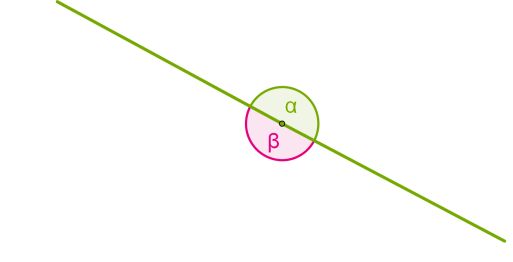 Внутрішньою областю розгорнутого кута можна вважати будь-яку з двох частин, на які він ділить площину. Якщо у внутрішній області кута провести промінь із початком у вершині цього кута, то промінь поділить кут на два кути.
Внутрішньою областю розгорнутого кута можна вважати будь-яку з двох частин, на які він ділить площину. Якщо у внутрішній області кута провести промінь із початком у вершині цього кута, то промінь поділить кут на два кути. 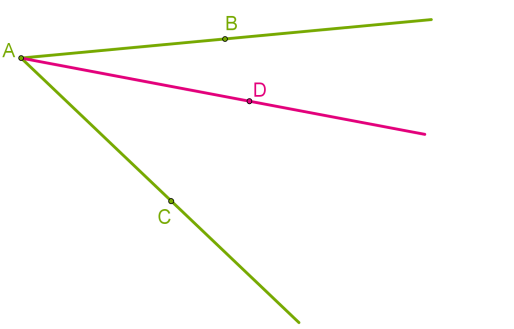 У такому випадку важливо правильно називати кути, оскільки ми маємо даний кут і дві його частини. Наприклад, не зовсім зрозуміло, про який кут ідеться, якщо записано
У такому випадку важливо правильно називати кути, оскільки ми маємо даний кут і дві його частини. Наприклад, не зовсім зрозуміло, про який кут ідеться, якщо записано ∠A . Краще використовувати три великі букви, тоді назви кутів будуть зрозумілі: ∠CAB , ∠CAD , ∠DAB






відрізки
Ми бачимо лише частини нескінченних прямих







Домашнє завдання :параграф 1-3 повторити , виконати вправи :
1. Відкладіть
на промені AN відрізки АВ = 2 см, АС = 5 см, АD= 9 см.
Знайдіть відстань між серединами відрізків АВ
і CD.
2. На
відрізку AD позначено точки В і С
так, що АВ = СD, AC=5 см. Знайдіть довжину відрізка BD.
3.
За допомогою транспортира поділіть на 3 рівні частини прямий кут та
розгорнутий кут.
4.
Точки A, B, C лежать на одній прямій AB=10см, відрізок АС у 6 разів більший
за відрізок BC. Знайди довжину AC.






















Немає коментарів:
Дописати коментар