Завдання на період з 16.05 по 20.05
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер 0960813579
Дата 18.05 Тема уроку :
"Елементи комбінаторики, теорії ймовірностей і математичної статистики."
Переглянути відео за посиланням :https://www.youtube.com/watch?v=e2-kUlMVnDM
Дата 16.05 Тема уроку :
"Інтеграл та його застосування."
Переглянути відео за посиланням :https://www.youtube.com/watch?v=4YehcNQQdcE
Припустимо, що на площині xОy дано фігуру, яку обмежує пряма Ox, прямі x=a,
x=b і графік невід'ємної функції f(x) на проміжку[a,b].
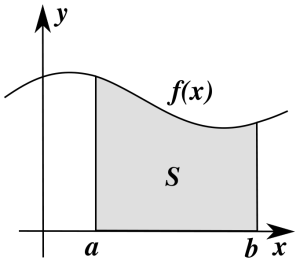
Площу цієї фігури можна обчислити, використовуючи формулу S=F(b)−F(a) , де F(x) є первісною функції f(x), тобто F'(x)=f(x) . Приклад:1) Обчисли площу фігури, обмеженої графіком функції f(x)=x2 на проміжку [1,2]. Розв'язанняДля функції f(x)=x2 однією з первісних є функція F(x)=x33 . Тоді шукана площаS=F(2)−F(1)=233−133=73
2) Обчисли площу фігури, обмеженої графіком функції y=lnx на проміжку [1,2].
Розв'язання
Спочатку знаходиться первісна даної функції (використовується метод інтегрування частинами).
∫lnxdx=[u=lnxdv=1du=dxxv=x]=∫udv=uv−∫vdu==lnx⋅x−∫(x⋅1x)dx=xlnx−∫dx=xlnx−x+C
Отже:
первісна функції — F(x)=xlnx−x ;
значення площі — S=F(2)−F(1)=(2ln2−2)−(1ln1−1)=2ln2−1 .

Домашнє завдання : № 25.400(1-4)
Завдання на період з 09.05 по 13.05
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер 0960813579
Дата 11.05 Тема уроку :
"Похідна функції. Застосування похідної до дослідження функцій."
Переглянути відео за посиланням :https://www.youtube.com/watch?v=KbxwehihPPk
Формулами диференціювання називають формули для знаходження похідних конкретних функцій, наприклад:
Теорема 1.
Якщо функції
Теорема 2.
Якщо функція
Теорема 3.
Якщо функції
На практиці цю теорему формулюють так:
похідна добутку двох функцій дорівнює сумі двох доданків; перший доданок є добуток похідної першої функції на другу функцію, а другий доданок є добуток першої функції на похідну другої функції.
Якщо функції
Домашнє завдання : № 25.377(1-6)
Дата 09.05 Тема уроку :
"Логарифмічні рівняння та нерівності"
Переглянути відео за посиланням :https://www.youtube.com/watch?v=joNOMMcr3SM
Для розв'язання даного рівняння, достатньо скористатися означенням логарифма, тобто подати число
Знайдене значення належить ОДЗ, отже, є коренем рівняння.
Розв'язання логарифмічних рівнянь типу logaf(x)=logag(x) зводиться до розв'язання рівняння f(x)=g(x) .Це випливає з монотонності логарифмічної функції. Потенціювання – це перехід від рівняння вигляду logaf(x)=logag(x) до рівняння f(x)=g(x) , де a - відмінне від одиниці додатне число, f(x) і g(x) - елементарні алгебраїчні функції, f(x)>0,g(x)>0. Для розв'язання даного типу рівнянь досить знайти всі корені рівняння f(x)=g(x) і серед отриманих, вибрати ті, що належать ОДЗ рівняння logaf(x)=logag(x) У випадку, якщо рівняння f(x)=g(x) коренів не має, тоді їх не має і вихідне логарифмічне рівняння.Приклад:Розв'яжи рівняння: log5(x+1)=log5(2x−3) Розв'язок.Знаходимо ОДЗ:{x+1>02x−3>0{x>−12x>3{x>−1x>1,5⇒x∈(1,5;+∞) Розв'язуємо рівнянняx+1=2x−3x−2x=−3−1−x=−4 x=4 належить інтервалу x∈(1,5;+∞) ,отже, є коренем вихідного логарифмічного рівняння.
Відповідь: x=4 Приклад:Розв'яжи рівняння log0,7(x+4)+log0,7(2x+3)=log0,7(1−2x) Розв'язок.ОДЗ:⎧⎩⎨⎪⎪x+4>02x+3>01−2x>0⎧⎩⎨⎪⎪x>−42x>−3−2x>−1⎧⎩⎨⎪⎪x>−4x>−1,5x<0,5⇒x∈(−1,5;0,5) log0,7(x+4)(2x+3)=log0,7(1−2x)(x+4)(2x+3)=1−2x2x2+8x+3x+12=1−2x2x2+13x+11=0x1=−1,x2=−5,5x1=−1∈ОДЗ x2=−5,5∉ОДЗ отже, −5,5 не є коренем вихідного рівняння.
Відповідь: x=−1
Відповідь:
Відповідь:
Рівняння вигляду f(logax)=0 розв'язуються за допомогою підстановки t=logax ,яка приводить рівняння до вигляду f(t)=0 .Якщо t – корінь рівняння f(t)=0 , тоді після повернення до підстановки t=logax ,можна знайти корінь вихідного логарифмічного рівняння,тобто x=at (аналогічно знаходяться й інші корені, якщо вони є). Приклад:Розв'язати рівняння:log22(x+4)=2log2(x+4)+3 Розв'язок:log22(x+4)=2log2(x+4)+3log2(x+4)=tt2−2t−3=0{t1+t2=2t1⋅t2=−3⇒{t1=−1t=3log2(x+4)=−12−1=x+40,5=x+40,5−4=xx=−3,5¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯log2(x+4)=323=x+48=x+48−4=xx=4¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ ОДЗ: x+4>0x>−4x∈(−4∈;+∞) x=−3,5 та x=4 обидва належать ОДЗВідповідь: −3,5;4 Приклад:Розв'язати рівняння: 2log24x−5log4x=−2 Розв'язок: 2log24x−5log4x+2=0 Позначивши log4x=t , отримаємо рівняння 2t2−5t+2=0 .Корені цього рівняння t1=12,t2=2 .Із рівняння log4x=12 знаходимо, що x=412=4–√=2 , а з рівняння log4x=2 , випливає, що x=42 , тобто x=16 .Обидва кореня належать ОДЗ:x>0 .Відповідь: 2;16 .Приклад:Завдання. Знайти корені рівняння logx(6−x)=2 Розв'язок.ОДЗ:⎧⎩⎨⎪⎪6−x>0x>0x≠1⎧⎩⎨⎪⎪−x>−6x>0x≠1⎧⎩⎨⎪⎪x<6x>0x≠1x∈(0;1)∪(1;6) Введемо нову змінну:6−x=tlogxt=2x2=t Повернемося до позначеногоx2=6−xx2+x−6=0x1=−3,x2=2 Перший корінь не належить ОДЗ, а отже коренем є x=2 Відповідь: x=2
Домашнє завдання : № 25.367
Завдання на період з 02.05 по 06.05
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер 0960813579
Дата 04.05 Тема уроку :
"Показникові рівняння та нерівності"
Переглянути відео за посиланням :https://www.youtube.com/watch?v=Rs5nq7a6ykw
Показникові рівняння
Показниковими називаються рівняння, в яких невідоме міститься в показнику степеня при сталих основах.
Наприклад: рівняння є показниковими.
Найпростішим показниковими рівнянням є рівняння .
Оскільки множина значень функції - множина додатних чисел, то рівняння :
1) має один корінь, якщо b>0;
2) не має коренів, якщо b≤0.
Для того, щоб розв’язати рівняння , треба b подати у вигляді , тобі будемо мати , звідси х=с.
Розглянемо приклади.
Приклад 1. Розв’яжіть рівняння .
Розв’язання
Оскільки , а , то маємо , звідси х=3.
Відповідь: 3.
Приклад 2. Розв’яжіть рівняння .
Розв’язання
Оскільки , то маємо , звідси х=-2.
Відповідь: -2.
Приклад 3. Розв’яжіть рівняння .
Розв’язання
Оскільки , то , звідси х1=2, х2=3.
Показникові нерівності
Розв’язування показникових нерівностей часто зводяться до розв’язування нерівностей або . Ці нерівності розв’язують, використовуючи монотонність (зростання, спадання) показникової функції.
Розглянемо приклади.
Приклад 1. Розв’яжіть нерівність .
Розв’язання
Запишемо дану нерівність у вигляді . Оскільки 3>1, то функція є зростаючою. Отже, при х<3 виконується нерівність .
Відповідь: (-∞;3).
Приклад 2. Розв’яжіть нерівність .
Розв’язання
Запишемо дану нерівність у вигляді . Оскільки – спадна функція, то .
Відповідь: .
Домашнє завдання : № 25.254
Дата 02.05 Тема уроку :
"Показникові рівняння та нерівності"
Переглянути відео за посиланням :https://www.youtube.com/watch?v=GU24bBp5sRo
Так що запис вигляду
Якщо
1.
2.
Справедливі наступні властивості (припускаємо, що
Можна виділити три основні методи розв'язання показникових рівнянь, які наводяться в наступних теоретичних матеріалах даного розділу.
Домашнє завдання : № 25.253
Завдання на період з 25.04 по 29.04
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер 0960813579
Дата 27.04 Тема уроку :
"Контрольна робота з теми: «Повторення»"
Виконати контрольну роботу за посиланням : https://docs.google.com/document/d/1Xkvy1d_L0oDY-zAL-RRqSgIF8TvPj0F8/edit?usp=sharing&ouid=114690071356165548445&rtpof=true&sd=true
Дата 25.04 Тема уроку :
"Узагальнення та систематизація знань, умінь і навичок учнів з теми: «Повторення»"
Переглянути відео за посиланням :https://www.youtube.com/watch?v=4yaBQUsquYE
Переглянути відео за посиланням :https://www.youtube.com/watch?v=5sJOOTzNeQA
Домашнє завдання : № 1
Розв'яжіть рівняння
1.√(х+2)=х
2. √(4х-5)=√(1-х)
3. √(15-3х)=х+1
4.√(2х-4)-√(х+5)=1
Розв'яжіть нерівність
1. √(х-3)>-2
2. √(х+5)<√(8-х)
3. √(х+18)<2-х
4. √(11-5х)≥х-1
Завдання на період з 18.04 по 22.04
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер 0960813579
Дата 20.04 Тема уроку :
"Розв’язування найпростіших тригонометричних нерівностей."
Переглянути відео за посиланням :https://www.youtube.com/watch?v=olOU7s6VALw
Дата 18.04 Тема уроку :
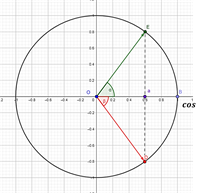
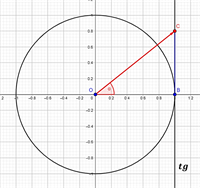
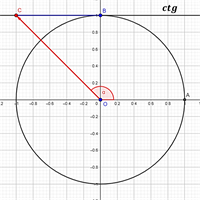
"Розв’язування найпростіших тригонометричних рівнянь."
Переглянути відео за посиланням :https://www.youtube.com/watch?v=4u7SD1RelJ8

Домашнє завдання : № 25.339, 25.340
Завдання на період з 11.04 по 15.04
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер 0960813579
Дата 13.04 Тема уроку :
"Тригонометричні формули"
Переглянути відео за посиланням : https://www.youtube.com/watch?v=Xpp_TRL3ZsU
Формули подвійного аргументу дозволяють представити тригонометричну функцію подвоєного аргументу у вигляді виразу тригонометричних функцій простого (одинарного) аргументу.Ці формули встановлюють співвідношення між sin 2x , cos 2x , tg 2x і sin x , cos x , tg x . Послідовно приведемо і доведемо формули подвійного аргументу для функцій синуса, косинуса і тангенса. 1. Розглянемо вираз sin 2x - представимо його аргумент у вигляді 2x=x+x і скористаємося відомою формулою синуса суми аргументів:sin(α+β)=sinα⋅cosβ+cosα⋅sinβ .Тоді отримаємо:sin2x=sin(x+x)=sinx⋅cosx+cosx⋅sinx=2sinx⋅cosx Отже, формула синуса подвійного аргументу: sin2x=2sinx⋅cosx 2. Розглянемо вираз cos 2x і аналогічно представимо його аргумент у вигляді 2x=x+x , а також скористаємося відомою формулою косинуса суми аргументів:cos(α+β)=cosα⋅cosβ−sinα⋅sinβ .Тоді отримаємо:cos2x=cos(x+x)=cosx⋅cosx−sinx⋅sinx=cos2x−sin2x Отже, формула косинуса подвійного аргументу: cos2x=cos2x−sin2x 3. Тепер розглянемо вираз tg 2x і знову представимо його аргумент у вигляді 2x=x+x , що дасть можливість скористатися відомою формулою тангенса суми аргументів: tg(α+β)=tgα+tgβ1−tgα⋅tgβ .Тоді отримаємо:tg2x=tg(x+x)=tgx+tgx1−tgx⋅tgx=2tgx1−tg2x формула тангенса подвійного аргументу: tg2x=2tgx1−tg2x Зверни увагу!Формули синуса подвійного аргументу і косинуса подвійного аргументу справедливі для будь-яких значень аргументу (ніяких обмежень немає), тоді, як формула тангенса подвійного аргументу справедлива лише для тих значень аргументу x , для яких визначені функції tg x і tg 2x , а також відмінний від нуля знаменник дробу, тобто 1−tg2x≠0 .Це рівнозначно одночасному виконанню умов: x≠π2+πk,k∈Z , x≠π4+πn,n∈Z . Зрозуміло, всі отримані формули можна застосувати й у тих випадках, коли місце аргументу x займає більш складний вираз, наприклад, справедливі наступні співвідношення: sin4x=2sin2x⋅cos2x sinx=2sinx2⋅cosx2 - до речі, цю формулу іноді називають формулою половинного аргументу cos48°=cos224°−sin224° cos(2x+6y)=cos2(x+3y)=cos2(x+3y)−sin2(x+3y) tg(2π3−2t)=tg(2(π3−t))=2tg(π3−t)1−tg2(π3−t) і т.п. Будь-яку з отриманих формул подвійного аргументу можна використовувати, як зліва направо, так і справа наліво (згортати) для розв'язання тригонометричних виразів .
Домашнє завдання : № 25.319
Дата 11.04 Тема уроку :
"Раціональні вирази"
Переглянути відео за посиланням : https://www.youtube.com/watch?v=mgNeFmRRIYs
Вирази, в яких є лише додавання, віднімання, множення змінних або зведення їх до степеня, називаються цілими раціональними алгебраїчними виразами.Приклад:2,6x+5y− z23 +3
z23 не є дробовим раціональним виразом, оскільки в знаменнику немає змінної.Вирази, в яких є ще й ділення змінних, називаються дробовими раціональними алгебраїчними виразами.Приклад:2x;4−yz+3;a3c;xx−5+x24+x — дробові раціональні вирази.
Дробові раціональні вирази мають область визначення з усіма значеннями змінних, що не перетворюють знаменник на 0 (тому що на 0 ділити не можна).
Область визначення — це множина, що складається з усіх допустимих значень змінної.Є завдання на знаходження області визначення, але під час розв'язання дробових раціональних рівнянь потрібно також обов'язково знаходити область визначення.Приклад:Знайди область визначення виразу x2−x
Розв’язання:2−x≠0−x≠−2x≠2 , значить, при x = 2 вираз не має сенсу.
Відповідь: область визначення виразу — x∈(−∞;2)∪(2;+∞)
Розв'яжи рівняння: x2+1x−1=2xx−1
Розв’язання:x2+1x−1=2xx−1x2+1=2xx2−2x+1=0D=0x1=x2=1 Отримані корені не належать області визначення рівняння.
Відповідь: немає коренів.
Для того, щоб скоротити алгебраїчний дріб, потрібно чисельник і знаменник розкласти на множники. Якщо виявиться, що чисельник і знаменник мають спільні множники, їх можна скоротити.Прийоми розкладання многочленів на множники:- винесення спільного множника за дужки;
- використання тотожностей скороченого множення;
- спосіб групування.
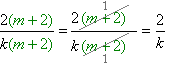
дріб скорочений на двочлен(m+2) ; 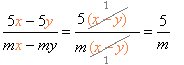
чисельник і знаменник дробу розкладені на множники, дріб скорочений на спільний множник (x–y) ; 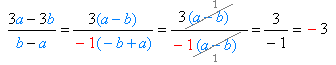
чисельник і знаменник дробу розкладені на множники, дріб скорочений на (a−b) ; 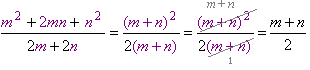
чисельник дробу розкладений на множники за допомогою формули квадрата суми; у знаменнику спільний множник винесено за дужки; дріб скорочений на спільний множник (m+n)
Тотожності скороченого множення, які можна використовувати при скороченні дробівРізниця квадратів: a2−b2=(a−b)(a+b) ;Квадрат суми: (a+b)2=a2+2ab+b2 ;Квадрат різниці: (a−b)2=a2−2ab+b2 ;Сума кубів: a3+b3=(a+b)(a2−ab+b2) ;Різниця кубів: a3−b3=(a−b)(a2+ab+b2)
Приклад:Скороти дріб: x2−4x2−4x+4
Розв'язання:
1. Чисельник і знаменник дробу розкладаємо на множники, використовуючи формули різниці квадратів і квадрата різниці.
x2−4x2−4x+4=(x−2)(x+2)(x−2)2 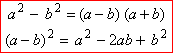
2. Скорочуємо дріб на загальний множник — двочлен (x−2)
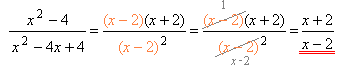 Приклад:Перетвори дріб
Приклад:Перетвори дріб 2x+2 таким чином, щоб у знаменнику було 3x2−12
Розв'язання:1. Аби зрозуміти, як розширити дріб 2x+2 , вираз 3x2−12 розкладаємо на множники.3x2−12=3(x2−4)=3(x−2)(x+2)
2. Порівнюємо отриманий вираз зі знаменником дробу x+2 та робимо висновок, що додатковим множником цього дробу є 3(x−2)
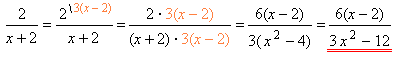 Приклад:Спрости вираз:
Приклад:Спрости вираз: 2x3+166x2−12x+24
Розв'язання:
1. У чисельнику за дужки виносимо спільний множник 2 , а в знаменнику — спільний множник 6
2x3+166x2−12x+24=2(x3+8)6(x2−2x+4)
2. Вираз x3+8 розкладаємо на множники, використовуючи формулу суми кубів, а потім дріб скорочуємо.
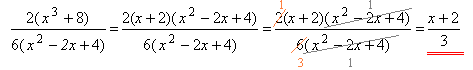
Рівні знаменники відкидаються. Знаходимо область визначення рівняння:x−1≠0x≠1
Відповідь: область визначення виразу —
Отримані корені не належать області визначення рівняння. Відповідь: немає коренів. Для того, щоб скоротити алгебраїчний дріб, потрібно чисельник і знаменник розкласти на множники. Якщо виявиться, що чисельник і знаменник мають спільні множники, їх можна скоротити. Прийоми розкладання многочленів на множники:
Тотожності скороченого множення, які можна використовувати при скороченні дробів Квадрат суми: Квадрат різниці: Сума кубів: Різниця кубів: Приклад: Скороти дріб: Розв'язання: 1. Чисельник і знаменник дробу розкладаємо на множники, використовуючи формули різниці квадратів і квадрата різниці. 2. Скорочуємо дріб на загальний множник — двочлен Приклад: Перетвори дріб Розв'язання: 1. Аби зрозуміти, як розширити дріб 2. Порівнюємо отриманий вираз зі знаменником дробу Приклад: Спрости вираз: Розв'язання: 1. У чисельнику за дужки виносимо спільний множник 2. Вираз | Рівні знаменники відкидаються. Знаходимо область визначення рівняння: |
Домашнє завдання : № 25.105
Завдання на період з 04.04 по 08.04
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер 0960813579
Дата 06.04 Тема уроку :
"Ірраціональні рівняння та нерівності"
Переглянути відео за посиланням :https://www.youtube.com/watch?v=onR-bXurfLA
Домашнє завдання : № 23.6, 23.8
Дата 04.04 Тема уроку :
"Ірраціональні рівняння та нерівності"
Переглянути відео за посиланням :https://www.youtube.com/watch?v=0xMsVngtSZE&ab_channel=MONUKRAINE
Опрацювати матеріал :
Зробимо перевірку отриманих коренів, для цього підставимо значення змінної
При
Отже, початкове ірраціональне рівняння має два корені.
Відповідь:
Домашнє завдання : № 25.254(1,3,5,7)
Завдання на період з 28.03 по 31.03
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер 0960813579
Дата 30.03 Тема уроку :
" Корінь n -го степеня.Степінь з раціональним показником"
Переглянути відео за посиланням :https://www.youtube.com/watch?v=5v2QWqY8bWg&ab_channel=MONUKRAINE
1. Поняття степеня з раціональним показником
Теорія:
Розв'язання
Розв'язання
Відповідь:
Розв'язання
Отже, зі знайдених вище двох значень
Відповідь:
Властивості степеня з раціональним показником
Теорія:
Розв'язання
Домашнє завдання : № 25.218 ; 25.222
Дата 28.03 Тема уроку :
"Функції , їх властивості та графіки "
Переглянути відео за посиланням :https://www.youtube.com/watch?v=NbY9Tc47eC8&ab_channel=MONUKRAINE
Домашнє завдання : № 25.260(1,2,3,4,9) стр.272
Завдання на період з 21.03 по 25.03
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер 0960813579
Дата 23.03 Тема уроку :
"Корекція знань,умінь та навичок"
Статистика займається збором, зображенням (у вигляді таблиць, діаграм, графіків та ін.) та аналізом інформації про різні випадкові величини.
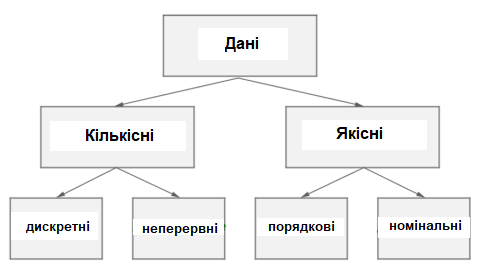
Для обробки даних вимірювання використовують графічне, візуальне зображення наявної інформації. Добре відомий табличний спосіб задання функцій.
Дані таблиці можна зобразити за допомогою так званої гістограми частот і полігону.
У частотній таблиці відображено чисельність робітників на різних заводах.
Чисельність робітників | |||||
Кількість заводів |
Гістограма частот:
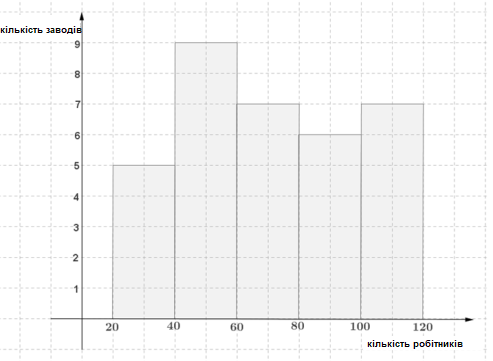
Полігон частот:
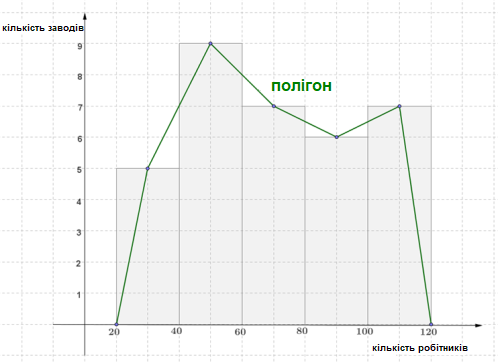
У статистиці досліджують різні сукупності даних — числових значень випадкових величин із урахуванням частот, із якими вони зустрічаються в сукупності.
При цьому сукупність усіх даних називають генеральною сукупністю, а будь-яку вибрану з неї частину — вибіркою.
Сукупність даних іноді буває корисно охарактеризувати (оцінити) одним числом — мірою центральної тенденції числових значень її елементів. До таких характеристик належать мода, медіана та середнє.
Mода вибірки
Якщо у впорядкованій вибірці парна кількість даних, то медіана дорівнює середньому арифметичному двох серединних чисел.
Якщо розглядається сукупність значень випадкової величини
Знайди середнє вибірки значень випадкової величини
Однією з найбільш поширених характеристик вибірки значень випадкової величини, чий розподіл за ймовірностями відомий, є так зване математичне очікування.
Нехай розподіл за ймовірностями
... | |||||
… |
Тоді число
Домашнє завдання : Параграф 16-20 повторити,
Дані подано в таблиці.
Значення ознаки (отримана кількість балів) | Частота (кількість учнів, які отримали відповідну кількість балів) |
0 | 5 |
1 | 5 |
2 | 1 |
3 | 3 |
4 | 3 |
Дата 21.03 Тема уроку : Контрольна робота з теми :"Елементи комбінаторики,теорії ймовірності та математичної статистики"
Виконати контрольну роботу за посиланням : https://docs.google.com/forms/d/e/1FAIpQLSfAV5TaT4FT_uffoOejB9tEPjytMgBaxSBgaX7U8ZRJdLNcWw/viewform?usp=sf_link
Домашнє завдання : Параграф 16-20 повторити
Завдання на період з 14.03 по 18.03
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер 0960813579
Дата 16.03 Тема уроку : "Узагальнення та систематизація знань умінь і навичок учнів з теми :Елементи комбінаторики,теорії ймовірності та математичної статистики""
Переглянути відео за посиланням :https://www.youtube.com/watch?v=tgOcIIJLcGE
Домашнє завдання : Параграф 16-20 повторити, сторінка 195-197 тести
Дата 14.03 Тема уроку : "Розвязування вправ. Самостійна робота"
Переглянути відео за посиланням :https://www.youtube.com/watch?v=rUm2PqOxB5g
Виконати самостійну роботу за посиланням : https://docs.google.com/forms/d/e/1FAIpQLScLjbk_J52KZ4DUQ39EM2YpzaQvLWcWLU1pAgPYriqOTZSAqA/viewform?usp=sf_link
Домашнє завдання : Параграф 20 повторити
Завдання на період з 11.10 по 15.10
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер 0960813579
Дата 13.10 Тема уроку : "Контрольна робота з теми "Показникова та логарифмічна функція""
Виконати контрольну роботу за посиланням : https://docs.google.com/document/d/1MXOomu7AGWLmv5DFkTpz7DPVCHW5uSba/edit?usp=sharing&ouid=114690071356165548445&rtpof=true&sd=true
Домашнє завдання : параграф 1-5 повторити
Дата 13.10 Тема уроку : "Контрольна робота з теми "Показникова та логарифмічна функція""
Виконати контрольну роботу за посиланням : https://docs.google.com/document/d/1MXOomu7AGWLmv5DFkTpz7DPVCHW5uSba/edit?usp=sharing&ouid=114690071356165548445&rtpof=true&sd=true
Домашнє завдання : параграф 1-5 повторити
Дата 11.10 Тема уроку : "Узагальнення та систематизація знань ,умінь і навичок учнів з теми : "Показникова та логарифмічна функція""
Переглянути відео за посиланням :https://www.youtube.com/watch?v=85LSs_rlmVc
Функція,
яку задано формулою y=ax,
де a>0, a≠1 називається
показниковою, а – основапоказникової функції. Якщо а=1, то функція y=ax=1x=1 є
сталою.
Графік функції у=ах
і у=(![]() )x симетричні відносно осі
ординат.
)x симетричні відносно осі
ординат.
Питання,
пов’язане з показниковою функцією, розробляв Леонард Ейлер
(15.04.1707-18.09.1783). Він народився у швейцарському Базелі в сім’ї
небагатого пастора Пауля Ейлера. Його мати Маргарита походила з освіченої
родини. Батько був математично обдарованою людиною й навіть написав дисертацію
про співвідношення і пропорції. Він і став першим учителем свого сина.
Незвичайна обдарованість хлопчика виявилася досить рано. У віці 13 років
Леонард вступив до Базельського університету, де слухав лекції з математики
Йоганна Бернуллі. А через чотири роки Ейлер – молодиймагістр філософії –
прочитав латиною свою першу лекцію про порівняльну характеристику філософії
Декарта і Ньютона.
Життя
вченого нараховує 60 років творчої діяльності. Ейлер написав близько 760 статей
для часописів, 40 книжок, а 15 його праць було підготовлено до різноманітних
конкурсів.
У двох
розділах своєї праці «Вступ до аналізу» він описав «показникові й логарифмічні
кількості». До перших належать ах, до других ух. Навіть і
сам показник може бути показниковою «кількістю», наприклад у виразах ![]() .
.
Ейлеру
належить відкриття зв’язку між показниковою і тригонометричними функціями.
Показникову
функцію виду у=ех почали
вивчати з 40 років XVII століття.
Іранський
математик ал – Караджі почав розглядати тричленні рівняння, квадратні відносно
деякого степеня невідомого, а також рівняння, що зводяться до них діленням на
степінь невідомого, тобто рівняння виду
ax2n+bxn=c, ax2n+c=bxn, bxn+c=ax2n, ax2n+m=bxn+m+cxn
2) До
слова запрошується віце-президент. Він називає основні властивості показникової
функції, розповідає про її застосування в інших галузях науки.
Властивості
показникової функції
-
Область визначення: всі
дійсні числа.
-
Область значень: усі
додатні числа.
-
Нулі: немає.
-
Проміжки
знакосталості: y>0 у всій області визначення; y<0 не існує.
-
Монотонність: якщо
а>1, функція зростає; якщо 0<a<1, функція спадає у всій області
визначення.
-
Парність,
непарність: функція загального виду
(функція ані парна, ані непарна).
-
Точка перетину з
віссю у: (0;1). З віссю х не перетинається.
-
Періодичність:
неперіодична.
-
Екстремуми: немає.
-
Графіком є
експонента.
«Експонента»
Як
запам’ятати наближене значення числа е
( експонента) ?
Вперше
позначення цієї константи літерою е ввів
Леонард Ейлер у 1727 році. Чому він позначив цю константу саме літерою е достеменно невідомо.
Можливо
це пов’язане з тим, що з неї починається слово exponenta (показниковий, експоненціальний). А може, тому що літери a,b,c,d
уже були «зайняті» і e виявилося
першою вільною?
e=2,718281828459045…
Домашнє завдання : параграф 1-5 повторити, виконати вправи: 2.18 , 3.11, 4.42 (1-3)
Завдання на період з 04.10 по 01.10
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер 0960813579
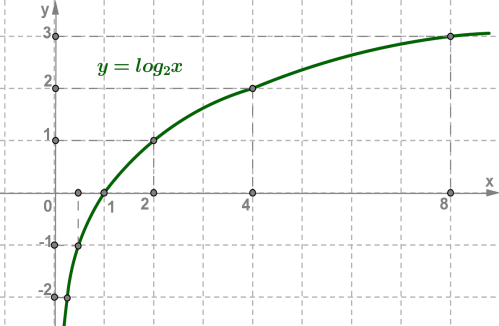
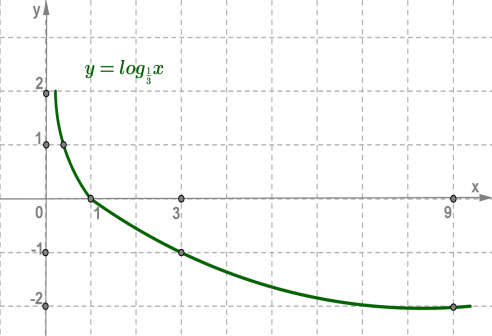
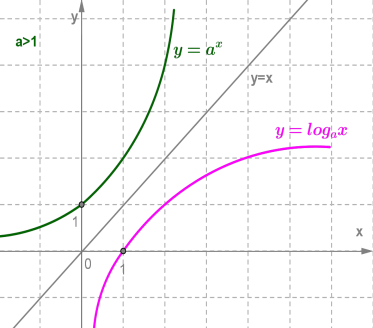
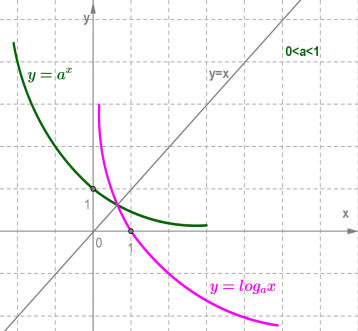
Дата 06.10 Тема уроку : "Властивості та графік логарифмічної функції"
Переглянути відео за посиланням :https://www.youtube.com/watch?v=pYETDnIUqKw
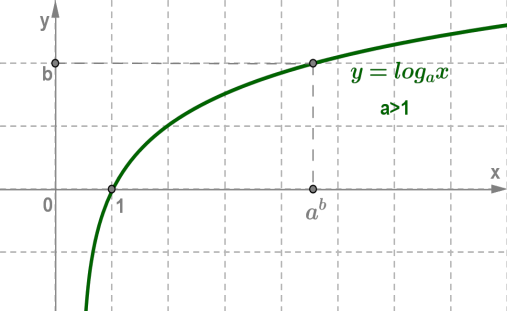
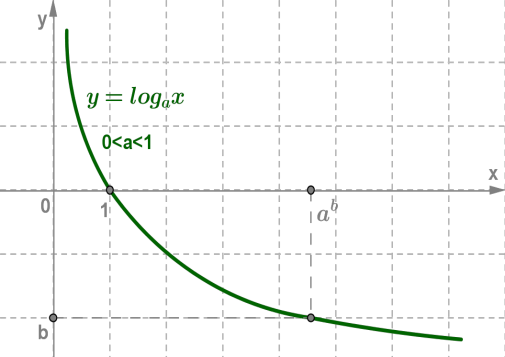
не має ні найбільшого, ні найменшого значень;
не обмежена зверху, не обмежена знизу;
| | | | | | | |
Домашнє завдання : параграф 5 опрацювати, виконати вправи: 5.16 , 5.28
Дата 04 .10 Тема уроку : "Розвязування вправ"
Переглянути відео за посиланням :https://www.youtube.com/watch?v=waYIBXIF6sI
Домашнє завдання : параграф 4 повторити, виконати вправи: 4.16, 4.24
Завдання на період з 27.09.по 01.10
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер 0960813579
Дата 29.09 Тема уроку : "Логарифми та їх властивості(натуральний логарифм)"
Переглянути відео за посиланням : https://www.youtube.com/watch?v=UQH6YFlzyXE
Логарифмом додатного числа b з основою a (a>0, a≠1) називається показник степеня, до якого треба піднести a, щоб отримати b.
logab
Наприклад: 25=32, отже, log232=5.
Види логарифмів
- loga b - логарифм числа b за основою a (a > 0, a ≠ 1, b > 0)
- lg b - десятковий логарифм (логарифм за основою 10, a = 10).
- ln b - натуральний логарифм (логарифм за основою e, a = e).
Основні властивості логарифмів описуються формулами:
Остання властивість називається основною властивістю логарифма.
Наведемо приклади застосування даних властивостей для перетворення логарифмічних виразів та знаходження їх значення:
Домашнє завдання : параграф 4 опрацювати, виконати вправи: 4.3 ,4.5
Дата 27.09 Тема уроку : "Розвязування вправ"
Переглянути відео за посиланням :https://www.youtube.com/watch?v=GU24bBp5sRo
Показникові рівняння :
Показниковими називаються рівняння, в яких невідоме міститься в показнику степеня при сталих основах.
Наприклад: рівняння 2х + 3 = 0; 3х+1 - 3х - 1 = 0 є показниковими.
Найпростішим показниковим рівнянням є рівняння ax = b, де а > 0, а ≠ 1.
Оскільки множина значень функції у = аx — множина додатних чисел, то рівняння:
Х = b:
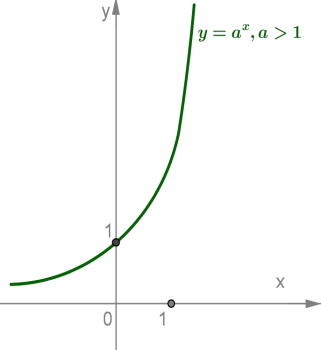
1) має один корінь, якщо b > 0 (рис. 2);
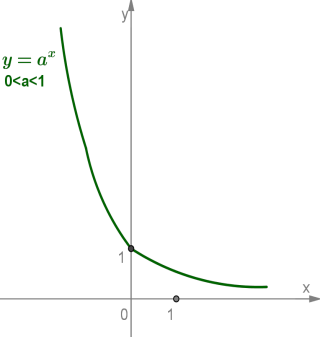
2) не має коренів, якщо b ≤ 0 (рис. 3).

Рис. 2

Рис. 3
Для того щоб розв’язати рівняння ax = b, де а > 0, а ≠ 1, b > 0, треба b подати у вигляді b = аc, тоді будемо мати аx = ac, звідси х = с.
Розглянемо приклади.
Приклад 1. Розв’яжіть рівняння 5x = 125.
Розв'язання :
Оскільки 5х = 125, а 125 = 53, то маємо 5х = 53, звідси х = 3.
Відповідь: 3.
Приклад 2. Розв’яжіть рівняння ( )x = 49.
)x = 49.
Оскільки 49 = 72 = ( )-2, то (
)-2, то ( )x = (
)x = ( )-2 звідси x = -2.
)-2 звідси x = -2.
Відповідь: -2.
Приклад 3. Розв’яжіть рівняння 15x2-5x+6 = 1.
Розв'язання
Оскільки 1 = 150, то 15х2-5х+6 = 150, x2 — 5X + 6 = 0, звідси x1 = 2, X2 = 3.
Відповідь: 2; 3.
Приклад 4. Розв’яжіть рівняння 2х-2 = -2.
Розв'язання
Оскільки 2х-2 > 0 при всіх знаменнях x, то рівняння коренів не має.
Відповідь: немає коренів.
Розглянемо деякі способи розв’язування показникових рівнянь.
І спосіб. Приведення рівняння до спільної основи, тобто до рівняння af(x) = аg(х).
Як відомо, показникова функція y = ax > 0 i а ≠ 1 монотонна, тому кожне своє значення вона приймає тільки при одному значенні аргументу. Із рівності af(x) = ag(x) випливає, що f(х) = g(x).
Приклад 1. Розв’яжіть рівняння 2х ∙ 5х = 0,1(10х-1)3.
Розв'язання
2х∙ 5х = 0,1(10х-1)3; 10х = 10-1∙ 103х-3; 10х = 103х-4; х = 3х - 4; х = 2.
Відповідь: 2.
ІІ спосіб. Винесення спільного множника за дужки.
Приклад 2. Розв’яжіть рівняння 3х - 2 ∙ 3х-2 = 63.
Розв'язання :
3x - 2 ∙ 3x-2 = 63; 3х-2 (32 - 2) = 63; 3х-2∙ 7 = 63; 3х-2 = 9; x - 2 = 2; x = 4.
Відповідь: 4.
Приклад 3. Розв’яжіть рівняння 52x-1 — 52x + 22x + 22x+2 = 0.
Розв'язання
22x + 22x+2 = 52x - 52x-1; 22x (1 +22) = 52x(1 - 5-1);
22x ∙ 5 = 52x ∙  ;
;  =
=  ; (
; ( )2x = (
)2x = ( )2 : 2x = ; x = 1.
)2 : 2x = ; x = 1.
Відповідь: 1.
IІІ спосіб. Приведення рівняння до квадратного.
Приклад 4. Розв'яжіть рівняння 49x - 8 ∙ 7x + 7 = 0.
Розв'язання
49x - 8 ∙ 7x + 7 = 0; (72)x - 8 ∙ 7x + 7 = 0; (7x)2- 8 ∙ 7x + 7 = 0.
Нехай 7х = t, тоді t2 - 8t + 7 = 0; t1 = 7; t2 = 1.
Отже. 1)7x = 7; х = 1; 2) 7x = 1; 7x = 70; x = 0.
Відповідь: 1; 0.
Приклад 5. Розв’яжіть рівняння 3 ∙ 16x + 2 ∙ 81x = 5 ∙ 36x.
Розв'язання
3 ∙ 42x + 2 ∙ 92x = 5 ∙ 4x ∙ 9x;  +
+  =
=  ; 3 ∙ (
; 3 ∙ ( )2x — 5 ∙ (
)2x — 5 ∙ ( )x + 3 = 0.
)x + 3 = 0.
Заміна ( )x = у, тоді 3у2 - 5у + 2 = 0, звідси у, =
)x = у, тоді 3у2 - 5у + 2 = 0, звідси у, =  ; y2 = 1.
; y2 = 1.
Отже, 1) ( )x =
)x =  ; (
; ( )2x =
)2x =  ; 2x = 1; x =
; 2x = 1; x =  ;
;
2) ( )x = 1; x = 0.
)x = 1; x = 0.
Відповідь: 0;  .
.
IV спосіб. Графічний спосіб розв’язування показникових рівнянь.
Приклад 6. Розв’яжіть графічно рівняння ( )x = х +1.
)x = х +1.
Розв'язання
Побудуємо графіки функцій у = ( )x, у = х + 1 в одній системі координат.
)x, у = х + 1 в одній системі координат.
Графіки функцій у = ( )x і у = х + 1 перегинаються в точці, абсциса якої х = 0 (рис. 4).
)x і у = х + 1 перегинаються в точці, абсциса якої х = 0 (рис. 4).
Відповідь: х = 0.

Рис. 4
Зауваження. Корінь цього рівняння легко знайти усно, однак треба пам'ятати, що в цьому випадку необхідно доводити той факт, що знайдений корінь єдиний.
Системи показникових рівнянь
При розв’язуванні систем показникових рівнянь використовуються традиційні способи розв’язування показникових рівнянь і знайомі Вам способи розв’язування систем рівнянь.
Розглянемо приклади.
Приклад 7. Розв’яжіть систему рівнянь 
Розв'язання
Зробимо заміну 3x = а, 7y = b, тоді матимемо систему:

Розв’яжемо систему рівнянь:



Отже, 

Відповідь: (2; 1).
Приклад 8. Розв’яжіть систему рівнянь 
Розв’язання 



 або
або 
 або
або 
Отже,  і
і  є розв’язками системи.
є розв’язками системи.
Відповідь: (1; 2), (2; 1).
Приклад 9. Розв’яжіть систему рівнянь 
Розв’язання
Перемножимо і розділимо рівняння системи, тоді одержимо:





Відповідь: (2; 1).
Показникові нерівності
Розв’язування показникових нерівностей часто зводяться до розв’язування нерівностей аx > ab (аx ≥ ab) або аx < ab (аx ≤ аb). Ці нерівності розв’язують, використовуючи монотонність (зростання, спадання) показникової функції.
Розглянемо приклади.
Приклад 10. Розв’яжіть нерівність 3x < 27.
Розв’язання
Запишемо дану нерівність у вигляді 3x < 33. Оскільки 3 > 1, то функція у = 3t є зростаючою. Отже, при х < 3 виконується нерівність 3x < 27.
Відповідь: (-∞; 3).
Приклад 11. Розв’яжіть нерівність ( )x >
)x >  .
.
Розв'язання
Запишемо дану нерівність у вигляді ( )x >
)x >  ; (
; ( )x >
)x >  .
.
Оскільки у = ( )x — спадна функція, то х < -
)x — спадна функція, то х < -  .
.
Відповідь: (-х; -  ).
).
Приклад 12. Розв’яжіть графічно нерівність 2х ≤ 3 - х.
Розв’язання :
Побудуємо графіки функцій у = 2х і у = 3 - х (рис. 5). Із рисунка видно, що 2х ≤ 3 - х при x ≤ 1. Отже, розв’язком нерівності 2х ≤ 3 - х є проміжок (-∞; 1 ]. Відповідь: (-∞; 1].

Рис. 5
Приклад 13. Розв’яжіть нерівність 6x2+2х > 63.
Розв’язання
Показникова функція у = 6t зростає, тому дана нерівність рівносильна нерівності х2 + 2x > 3. Розв’язуємо нерівність x2 + 2X - 3 >0 методом інтервалів (рис. 6).
Маємо X∈ (-∞; -3) (1; +∞).
(1; +∞).
Відповідь: (-∞; -3) ( 1; +∞).
( 1; +∞).

Рис. 6
Приклад 14. Розв’яжіть нерівність 25x + 25 ∙ 5x - 1250 > 0.
Розв’язання
Зробимо заміну 5x = t, тоді дану нерівність запишемо так:
t2 + 25t - 1250 >0.
Розв’яжемо одержану нерівність методом інтервалів (рис. 7), тоді
t <-50 або t > 25.
Отже, маємо дві нерівності: 5x < -50 або 5x > 25.
Розв’яжемо їх:
1) 5x < -50 — розв'язків немає;
2) 5x > 25; 5x > 52; X > 2.
Відповідь: (2; +∞).

Рис. 7
Показникові рівняння :
Показниковими називаються рівняння, в яких невідоме міститься в показнику степеня при сталих основах.
Наприклад: рівняння 2х + 3 = 0; 3х+1 - 3х - 1 = 0 є показниковими.
Найпростішим показниковим рівнянням є рівняння ax = b, де а > 0, а ≠ 1.
Оскільки множина значень функції у = аx — множина додатних чисел, то рівняння:
Х = b:
1) має один корінь, якщо b > 0 (рис. 2);
2) не має коренів, якщо b ≤ 0 (рис. 3).

Рис. 2

Рис. 3
Для того щоб розв’язати рівняння ax = b, де а > 0, а ≠ 1, b > 0, треба b подати у вигляді b = аc, тоді будемо мати аx = ac, звідси х = с.
Розглянемо приклади.
Приклад 1. Розв’яжіть рівняння 5x = 125.
Розв'язання :
Оскільки 5х = 125, а 125 = 53, то маємо 5х = 53, звідси х = 3.
Відповідь: 3.
Приклад 2. Розв’яжіть рівняння (![]() )x = 49.
)x = 49.
Оскільки 49 = 72 = (![]() )-2, то (
)-2, то (![]() )x = (
)x = (![]() )-2 звідси x = -2.
)-2 звідси x = -2.
Відповідь: -2.
Приклад 3. Розв’яжіть рівняння 15x2-5x+6 = 1.
Розв'язання
Оскільки 1 = 150, то 15х2-5х+6 = 150, x2 — 5X + 6 = 0, звідси x1 = 2, X2 = 3.
Відповідь: 2; 3.
Приклад 4. Розв’яжіть рівняння 2х-2 = -2.
Розв'язання
Оскільки 2х-2 > 0 при всіх знаменнях x, то рівняння коренів не має.
Відповідь: немає коренів.
Розглянемо деякі способи розв’язування показникових рівнянь.
І спосіб. Приведення рівняння до спільної основи, тобто до рівняння af(x) = аg(х).
Як відомо, показникова функція y = ax > 0 i а ≠ 1 монотонна, тому кожне своє значення вона приймає тільки при одному значенні аргументу. Із рівності af(x) = ag(x) випливає, що f(х) = g(x).
Приклад 1. Розв’яжіть рівняння 2х ∙ 5х = 0,1(10х-1)3.
Розв'язання
2х∙ 5х = 0,1(10х-1)3; 10х = 10-1∙ 103х-3; 10х = 103х-4; х = 3х - 4; х = 2.
Відповідь: 2.
ІІ спосіб. Винесення спільного множника за дужки.
Приклад 2. Розв’яжіть рівняння 3х - 2 ∙ 3х-2 = 63.
Розв'язання :
3x - 2 ∙ 3x-2 = 63; 3х-2 (32 - 2) = 63; 3х-2∙ 7 = 63; 3х-2 = 9; x - 2 = 2; x = 4.
Відповідь: 4.
Приклад 3. Розв’яжіть рівняння 52x-1 — 52x + 22x + 22x+2 = 0.
Розв'язання
22x + 22x+2 = 52x - 52x-1; 22x (1 +22) = 52x(1 - 5-1);
22x ∙ 5 = 52x ∙ ![]() ;
; ![]() =
= ![]() ; (
; (![]() )2x = (
)2x = (![]() )2 : 2x = ; x = 1.
)2 : 2x = ; x = 1.
Відповідь: 1.
IІІ спосіб. Приведення рівняння до квадратного.
Приклад 4. Розв'яжіть рівняння 49x - 8 ∙ 7x + 7 = 0.
Розв'язання
49x - 8 ∙ 7x + 7 = 0; (72)x - 8 ∙ 7x + 7 = 0; (7x)2- 8 ∙ 7x + 7 = 0.
Нехай 7х = t, тоді t2 - 8t + 7 = 0; t1 = 7; t2 = 1.
Отже. 1)7x = 7; х = 1; 2) 7x = 1; 7x = 70; x = 0.
Відповідь: 1; 0.
Приклад 5. Розв’яжіть рівняння 3 ∙ 16x + 2 ∙ 81x = 5 ∙ 36x.
Розв'язання
3 ∙ 42x + 2 ∙ 92x = 5 ∙ 4x ∙ 9x; ![]() +
+ ![]() =
= ![]() ; 3 ∙ (
; 3 ∙ (![]() )2x — 5 ∙ (
)2x — 5 ∙ (![]() )x + 3 = 0.
)x + 3 = 0.
Заміна (![]() )x = у, тоді 3у2 - 5у + 2 = 0, звідси у, =
)x = у, тоді 3у2 - 5у + 2 = 0, звідси у, = ![]() ; y2 = 1.
; y2 = 1.
Отже, 1) (![]() )x =
)x = ![]() ; (
; (![]() )2x =
)2x = ![]() ; 2x = 1; x =
; 2x = 1; x = ![]() ;
;
2) (![]() )x = 1; x = 0.
)x = 1; x = 0.
Відповідь: 0; ![]() .
.
IV спосіб. Графічний спосіб розв’язування показникових рівнянь.
Приклад 6. Розв’яжіть графічно рівняння (![]() )x = х +1.
)x = х +1.
Розв'язання
Побудуємо графіки функцій у = (![]() )x, у = х + 1 в одній системі координат.
)x, у = х + 1 в одній системі координат.
Графіки функцій у = (![]() )x і у = х + 1 перегинаються в точці, абсциса якої х = 0 (рис. 4).
)x і у = х + 1 перегинаються в точці, абсциса якої х = 0 (рис. 4).
Відповідь: х = 0.

Рис. 4
Зауваження. Корінь цього рівняння легко знайти усно, однак треба пам'ятати, що в цьому випадку необхідно доводити той факт, що знайдений корінь єдиний.
Системи показникових рівнянь
При розв’язуванні систем показникових рівнянь використовуються традиційні способи розв’язування показникових рівнянь і знайомі Вам способи розв’язування систем рівнянь.
Розглянемо приклади.
Приклад 7. Розв’яжіть систему рівнянь ![]()
Розв'язання
Зробимо заміну 3x = а, 7y = b, тоді матимемо систему:
![]()
Розв’яжемо систему рівнянь:![]()
![]()
![]()
Отже, ![]()
![]()
Відповідь: (2; 1).
Приклад 8. Розв’яжіть систему рівнянь ![]()
Розв’язання ![]()
![]()
![]()
![]()
![]() або
або ![]()
![]() або
або ![]()
Отже, ![]() і
і ![]() є розв’язками системи.
є розв’язками системи.
Відповідь: (1; 2), (2; 1).
Приклад 9. Розв’яжіть систему рівнянь ![]()
Розв’язання
Перемножимо і розділимо рівняння системи, тоді одержимо:
![]()
![]()
![]()
![]()
![]()
Відповідь: (2; 1).
Показникові нерівності
Розв’язування показникових нерівностей часто зводяться до розв’язування нерівностей аx > ab (аx ≥ ab) або аx < ab (аx ≤ аb). Ці нерівності розв’язують, використовуючи монотонність (зростання, спадання) показникової функції.
Розглянемо приклади.
Приклад 10. Розв’яжіть нерівність 3x < 27.
Розв’язання
Запишемо дану нерівність у вигляді 3x < 33. Оскільки 3 > 1, то функція у = 3t є зростаючою. Отже, при х < 3 виконується нерівність 3x < 27.
Відповідь: (-∞; 3).
Приклад 11. Розв’яжіть нерівність (![]() )x >
)x > ![]() .
.
Розв'язання
Запишемо дану нерівність у вигляді (![]() )x >
)x > ![]() ; (
; (![]() )x >
)x > ![]() .
.
Оскільки у = (![]() )x — спадна функція, то х < -
)x — спадна функція, то х < - ![]() .
.
Відповідь: (-х; - ![]() ).
).
Приклад 12. Розв’яжіть графічно нерівність 2х ≤ 3 - х.
Розв’язання :
Побудуємо графіки функцій у = 2х і у = 3 - х (рис. 5). Із рисунка видно, що 2х ≤ 3 - х при x ≤ 1. Отже, розв’язком нерівності 2х ≤ 3 - х є проміжок (-∞; 1 ]. Відповідь: (-∞; 1].

Рис. 5
Приклад 13. Розв’яжіть нерівність 6x2+2х > 63.
Розв’язання
Показникова функція у = 6t зростає, тому дана нерівність рівносильна нерівності х2 + 2x > 3. Розв’язуємо нерівність x2 + 2X - 3 >0 методом інтервалів (рис. 6).
Маємо X∈ (-∞; -3)![]() (1; +∞).
(1; +∞).
Відповідь: (-∞; -3)![]() ( 1; +∞).
( 1; +∞).
![]()
Рис. 6
Приклад 14. Розв’яжіть нерівність 25x + 25 ∙ 5x - 1250 > 0.
Розв’язання
Зробимо заміну 5x = t, тоді дану нерівність запишемо так:
t2 + 25t - 1250 >0.
Розв’яжемо одержану нерівність методом інтервалів (рис. 7), тоді
t <-50 або t > 25.
Отже, маємо дві нерівності: 5x < -50 або 5x > 25.
Розв’яжемо їх:
1) 5x < -50 — розв'язків немає;
2) 5x > 25; 5x > 52; X > 2.
Відповідь: (2; +∞).
![]()
Рис. 7











Немає коментарів:
Дописати коментар