Завдання на період з 16.05 по 20.05 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 17.05
Tема : " Розв’язування задач на обчислення об’ємів та площ поверхонь тіл обертання"
Переглянути відео за посиланням : https://www.youtube.com/watch?v=Iedn-YfsnDk
1. Що таке циліндр?
Циліндр - це геометричне тіло, що складається із двох кругів, які не лежать в одній площині і суміщаються паралельним перенесенням, і всіх відрізків, що сполучають відповідні точки цих кругів.2. За якою формулою можна обчислити об’єм циліндра?
Об'єм циліндра дорівнює добутку площі його
основи на висоту:
, де R – радіус, а H – висота циліндра3. Що таке конус?Конус – це геометричне тіло, що складається з круга, точки, яка не лежить у площині цього круга і всіх відрізків, що сполучають цю точку з точками круга.4. Що таке твірні конуса?
Твірні - відрізки, що з'єднують вершину з точками
основи.
5. Що таке висота конуса?Висота - перпендикуляр, проведений з вершини до центра основи6. Чому дорівнює площа бічної поверхні конуса?
Площа бічної поверхні конуса дорівнює
половині добутку довжини кола основи на твірну:
де l - твірна.
7. Чому дорівнює об’єм конуса?
Об'єм конуса дорівнює одній третій добутку
площі його основи
на висоту:
8. Дайте означення кулі та її елементів
Кулею називається тіло, що складається з усіх точок
простору, відстань від яких до даної точки не перевищує заданої. Ця точка - центр кулі. Радіус - задана відстань.
Поверхня кулі називається сферою.
9. Чому дорівнює об’єм кулі?
Об'єм кулі дорівнює добутку площі її
поверхні на третину радіуса:
1. Що таке циліндр?
Циліндр - це геометричне тіло, що складається із двох кругів, які не лежать в одній площині і суміщаються паралельним перенесенням, і всіх відрізків, що сполучають відповідні точки цих кругів.2. За якою формулою можна обчислити об’єм циліндра?
Об'єм циліндра дорівнює добутку площі його
основи на висоту:
, де R – радіус, а H – висота циліндра3. Що таке конус?Конус – це геометричне тіло, що складається з круга, точки, яка не лежить у площині цього круга і всіх відрізків, що сполучають цю точку з точками круга.4. Що таке твірні конуса?
Твірні - відрізки, що з'єднують вершину з точками
основи.
5. Що таке висота конуса?Висота - перпендикуляр, проведений з вершини до центра основи6. Чому дорівнює площа бічної поверхні конуса?
Площа бічної поверхні конуса дорівнює
половині добутку довжини кола основи на твірну:
де l - твірна.
7. Чому дорівнює об’єм конуса?
Об'єм конуса дорівнює одній третій добутку площі його основи
на висоту:
8. Дайте означення кулі та її елементів
Кулею називається тіло, що складається з усіх точок
простору, відстань від яких до даної точки не перевищує заданої. Ця точка - центр кулі. Радіус - задана відстань.
Поверхня кулі називається сферою.
9. Чому дорівнює об’єм кулі?
Об'єм кулі дорівнює добутку площі її
поверхні на третину радіуса:
Домашнє задання : виконати вправи :
Задача 1. Вода – основа їжі. Без води людина може прожити не більше трьох
днів. Для нормального функціонування організму дев’ятикласник повинен
вживати щоденно 2,5л води. Скільки кружок води вип’є школяр за день,
якщо вона має форму циліндра висотою 10 см і діаметром 8 см?
Задача 2. Кімната має розміри 10м×6,5м×4м.
Обчисліть площу стін, які необхідно побілити, якщо площа вікон і дверей
становить 0,2 площі стін
Задача 3. Скільки метрів води вміщує бак циліндричної форми, якщо радіус
його основи дорівнює 30 см, а висота дорівнює 0,6м?
Завдання на період з 09.05 по 13.05 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 12.05
Tема : " Тіла обертання. Площі поверхонь та об’єми тіл обертання."
Переглянути відео за посиланням : https://www.youtube.com/watch?v=Iedn-YfsnDk
Циліндр
Циліндр (грец. Κύλινδρος - «валик») - геометричне тіло, обмежене замкнутою циліндричною поверхнею і двома паралельними площинами, що перетинають її.
- якщо основи циліндра пласкі - циліндр називають таким, що стоїть на площині;
- якщо основи стоять на площині циліндра і перпендикулярні твірним - прямий циліндр; зокрема якщо основа, що стоїть на площині циліндра:
- коло - круглий циліндр;
- еліпс - еліптичний циліндр.
Елементи циліндра
Круги, що утворюють циліндр, називаються основами циліндра. Вони рівні й лежать у паралельних площинах.
Твірні циліндра - відрізки, що сполучають відповідні точки кіл кругів. Вони паралельні й рівні між собою.
Поверхня циліндра складається з основ і бічної поверхні. Бічна поверхня складається з твірних.
Радіусом циліндра називається радіус його основи. Висотою циліндра називається відстань між площинами основ.
Віссю циліндра називається пряма, яка проходить через центри основ. Вона паралельна твірним.
Осьовий переріз - переріз циліндра площиною, яка проходить через вісь циліндра.
Дотична до циліндра - площина, яка проходить через твірну прямого циліндра і перпендикулярна до осьового перерізу, проведеного через цю твірну, називається площиною. Циліндр називається прямим, якщо його твірні перпендикулярні до площин основ. Прямий циліндр можна розглядати як тіло, утворене обертанням прямокутника навколо його сторони як осі.
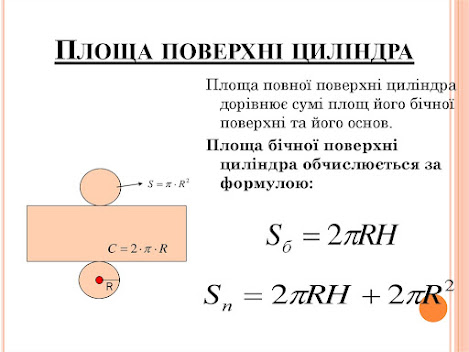
Площа поверхні циліндра
Площа бічної поверхні тіл обертання обчислюється за їхньою розгорткою.
Розгортка циліндра – це прямокутник з висотою h і довжиною 2?R, отже, площа
бічної поверхні циліндра дорівнює площі його розгортки та обчислюється за фор-
мулою:
Sh = 2πRh,
Площа повної поверхні циліндра дорівнює сумі площ його бічної поверхні та
його основ:
Sp = 2πR(h + R).
Конус
Ко́нус (від грец. Κώνος - «соснова шишка») - геометричне тіло, отримане шляхом об’єднання всіх променів, що виходять з однієї точки - вершини конуса, і таких, що проходять через довільну пласку поверхню. Іноді конусом називають частину такого тіла, отриману об’єднанням усіх відрізків, що з’єднують вершину і точки пласкої поверхні (яку в такому разі називають основою конуса, а конус називають таким, що спирається на дану поверхню). Також можна сказати, що це тіло, отримане при обертанні прямокутного трикутника навколо одного з його катетів.
Відрізок, опущений перпендикулярно з вершини на площину основи (а також його довжина), називається висотою конуса. Якщо площа основи має скінченне значення, то об’єм конуса також має скінченне значення й дорівнює третині добутку висоти на площу основи. Отже, всі конуси, що спираються на дану основу і мають вершину в площині, паралельній цій основі, мають рівний об’єм, оскільки їх висоти рівні. Якщо основою конуса є многокутник, тоді конус стає пірамідою. Таким чином піраміди є підмножиною конусів.
Відрізок, що сполучає вершину конуса з точкою границі його основи, називається твірною конуса. Множина всіх твірних конуса називається бічною поверхнею конуса.
Площа поверхні конуса
Повна площа прямого кругового конуса
S = πr(r + l),
де r і l – радіус кола основи і довжина твірної бічної поверхні відповідно.
Площа бічної поверхні прямого кругового конуса
Sb = πrl,
де r і l – радіус кола основи і довжина твірної бічної поверхні відповідно.
Куля
Куля - тіло, утворене обертанням круга навколо його діаметра. Центром кулі називають центр круга, обертанням якого її утворено. Відрізок, який сполучає центр кулі з довільною точкою її поверхні, - радіус кулі. Відрізок, який сполучає дві довільні точки поверхні кулі, - її хорда. Хорда кулі, яка проходить через центр, - діаметр кулі.
Куля - це множина всіх точок простору, що перебувають від заданої точки O на відстані, не більшій за дану відстань R. При цьому точка O називається центром, а R - радіусом кулі. Будь-який відрізок, який сполучає центр кулі з точкою кульової поверхні, також називається радіусом.
Поверхня кулі називається сферою. Також дуже часто кулею називають частину простору, обмежену сферою.
Площу сфери, яка обмежує кулю з радіусом R, можна підрахувати за формулою
S = 4πR2.
Площа поверхні кулі є найменшою серед площ поверхонь стереометричних тіл з однаковим об’ємом.
Циліндр
Циліндр (грец. Κύλινδρος - «валик») - геометричне тіло, обмежене замкнутою циліндричною поверхнею і двома паралельними площинами, що перетинають її.
- якщо основи циліндра пласкі - циліндр називають таким, що стоїть на площині;
- якщо основи стоять на площині циліндра і перпендикулярні твірним - прямий циліндр; зокрема якщо основа, що стоїть на площині циліндра:
- коло - круглий циліндр;
- еліпс - еліптичний циліндр.
Елементи циліндра
Круги, що утворюють циліндр, називаються основами циліндра. Вони рівні й лежать у паралельних площинах.
Твірні циліндра - відрізки, що сполучають відповідні точки кіл кругів. Вони паралельні й рівні між собою.
Поверхня циліндра складається з основ і бічної поверхні. Бічна поверхня складається з твірних.
Радіусом циліндра називається радіус його основи. Висотою циліндра називається відстань між площинами основ.
Віссю циліндра називається пряма, яка проходить через центри основ. Вона паралельна твірним.
Осьовий переріз - переріз циліндра площиною, яка проходить через вісь циліндра.
Дотична до циліндра - площина, яка проходить через твірну прямого циліндра і перпендикулярна до осьового перерізу, проведеного через цю твірну, називається площиною. Циліндр називається прямим, якщо його твірні перпендикулярні до площин основ. Прямий циліндр можна розглядати як тіло, утворене обертанням прямокутника навколо його сторони як осі.
Площа поверхні циліндра
Площа бічної поверхні тіл обертання обчислюється за їхньою розгорткою.
Розгортка циліндра – це прямокутник з висотою h і довжиною 2?R, отже, площа
бічної поверхні циліндра дорівнює площі його розгортки та обчислюється за фор-
мулою:
Sh = 2πRh,
Площа повної поверхні циліндра дорівнює сумі площ його бічної поверхні та
його основ:
Sp = 2πR(h + R).
Конус
Ко́нус (від грец. Κώνος - «соснова шишка») - геометричне тіло, отримане шляхом об’єднання всіх променів, що виходять з однієї точки - вершини конуса, і таких, що проходять через довільну пласку поверхню. Іноді конусом називають частину такого тіла, отриману об’єднанням усіх відрізків, що з’єднують вершину і точки пласкої поверхні (яку в такому разі називають основою конуса, а конус називають таким, що спирається на дану поверхню). Також можна сказати, що це тіло, отримане при обертанні прямокутного трикутника навколо одного з його катетів.
Відрізок, опущений перпендикулярно з вершини на площину основи (а також його довжина), називається висотою конуса. Якщо площа основи має скінченне значення, то об’єм конуса також має скінченне значення й дорівнює третині добутку висоти на площу основи. Отже, всі конуси, що спираються на дану основу і мають вершину в площині, паралельній цій основі, мають рівний об’єм, оскільки їх висоти рівні. Якщо основою конуса є многокутник, тоді конус стає пірамідою. Таким чином піраміди є підмножиною конусів.
Відрізок, що сполучає вершину конуса з точкою границі його основи, називається твірною конуса. Множина всіх твірних конуса називається бічною поверхнею конуса.
Площа поверхні конуса
Повна площа прямого кругового конуса
S = πr(r + l),
де r і l – радіус кола основи і довжина твірної бічної поверхні відповідно.
Площа бічної поверхні прямого кругового конуса
Sb = πrl,
де r і l – радіус кола основи і довжина твірної бічної поверхні відповідно.
Куля
Куля - тіло, утворене обертанням круга навколо його діаметра. Центром кулі називають центр круга, обертанням якого її утворено. Відрізок, який сполучає центр кулі з довільною точкою її поверхні, - радіус кулі. Відрізок, який сполучає дві довільні точки поверхні кулі, - її хорда. Хорда кулі, яка проходить через центр, - діаметр кулі.
Куля - це множина всіх точок простору, що перебувають від заданої точки O на відстані, не більшій за дану відстань R. При цьому точка O називається центром, а R - радіусом кулі. Будь-який відрізок, який сполучає центр кулі з точкою кульової поверхні, також називається радіусом.
Поверхня кулі називається сферою. Також дуже часто кулею називають частину простору, обмежену сферою.
Площу сфери, яка обмежує кулю з радіусом R, можна підрахувати за формулою
S = 4πR2.
Площа поверхні кулі є найменшою серед площ поверхонь стереометричних тіл з однаковим об’ємом.
Домашнє задання : виконати вправи :
І задача: Висота конуса
дорівнює 4 см, а радіус основи – 3 см. Знайдіть відношення площі основи конуса
до площі його бічної поверхні. (Відповідь запишіть десятковим дробом).
ІІ задача: Копиця сіна має
форму циліндра з конічним верхом. Радіус основи копиці дорівнює 2 м, висота
копиці – 3 м. Циліндрична частина має висоту 2,4 м. Знайдіть масу сіна у
копиці, якщо маса 1 м3 сіна становить 30 кг.
І задача: Висота конуса
дорівнює 4 см, а радіус основи – 3 см. Знайдіть відношення площі основи конуса
до площі його бічної поверхні. (Відповідь запишіть десятковим дробом).
ІІ задача: Копиця сіна має
форму циліндра з конічним верхом. Радіус основи копиці дорівнює 2 м, висота
копиці – 3 м. Циліндрична частина має висоту 2,4 м. Знайдіть масу сіна у
копиці, якщо маса 1 м3 сіна становить 30 кг.
Дата 10.05
Tема : "Корекція знань , умінь та навичок. Тіла обертання. Площі поверхонь та об’єми тіл обертання."
Переглянути відео за посиланням : https://www.youtube.com/watch?v=t-IkqCptS7E
Переглянути відео за посиланням :https://www.youtube.com/watch?v=MG7QSr3N7xg
Опрацювати матеріал :
Домашнє задання : виконати вправи :
Задача 2 : Знайдіть площу конуса з радіусом 13 см, якщо його твірна дорівнює 28 см.
Задача 3 : Радіус основи циліндра 2 м, висота – 3 м. Знайдіть діагональ та площу осьового перерізу.
Задача 4 : Знайдіть площу основи конуса, твірна
якого дорівнює 12 см, а площа бічної поверхні
- 504![]() см2.
см2.
Завдання на період з 02.05 по 06.05 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 05.05
Tема : "Контрольна робота з теми: «Многогранники. Площі поверхонь та об’єми многогранників. Повторення»"
Виконати контрольну роботу за посиланням : https://docs.google.com/document/d/1nUXiksyQLQYgQkkPLsBbU5rmAJ7Dw1VS/edit?usp=sharing&ouid=114690071356165548445&rtpof=true&sd=true
Домашнє задання : виконати контрольну роботу
Дата 03.05
Tема : "Узагальнення та систематизація знань, умінь і навичок учнів з теми: «Многогранники. Площі поверхонь та об’єми многогранників. Повторення»"
Переглянути відео за посиланням : https://www.youtube.com/watch?v=gG18rpwHQtI
Опрацювати матеріал:
Оформи опорний конспект
|
Геометричні тіла |
Площа бічної поверхні |
Площа повної поверхні |
Об’єм |
|
Пряма призма (Р–периметр
основи, l – довжина
ребра) |
Sбіч. = Р· l
|
Sп. = 2Sосн.+ Sбіч. |
V = Sосн. · H ( H – висота призми) |
|
Куб |
|
Sп. = 6а2 |
V = а3 ( а – ребро
куба) |
|
Піраміда |
Сума площ усіх бічних граней |
Sп. = Sосн.+ Sбіч |
V = ( H – висота піраміди) |
|
Правильна піраміда ( l –апофема) |
Sбіч. =
|
1. Окремі випадки розміщення висоти піраміди:
а) піраміди, висота
яких належить одній або двом бічним граням;
б) піраміди, основою
висоти яких є центр кола, описаного навколо основи піраміди;
в) піраміди, основою
висоти яких є цент кола, вписаного в основу піраміди
Домашнє задання : опрацювати теорію, виконати вправи :
Задача 1
1. Основним перерізом конуса є прямокутний трикутник з гіпотенузою 10см. Обчислити об’єм цього конуса.
Задача 2
2. Скільки метрів матерії шириною
Задача 3
3. Визначити об’єм піраміди Хеопса,
кола відомо, що в її основі лежить
квадрат із стороною
Завдання на період з 25.04 по 29.04 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 28.04
Tема : "Многогранники. Площі поверхонь та об’єми многогранників."
Переглянути відео за посиланням : https://www.youtube.com/watch?v=peCwtumSdnU
Домашнє задання : опрацювати теорію, виконати вправи :
Задача 1
Дата 26.04
Tема : "Многогранники. Площі поверхонь та об’єми многогранників."
Переглянути відео за посиланням : https://www.youtube.com/watch?v=9KKUZPe8Hwk
Опрацювати матеріал :
Домашнє задання : опрацювати теорію, виконати вправи
1.
Призма
в основі якої лежить ромб, діагоналі
якого 20 см і 14 см. Бічне ребро 12 см. Знайти повну поверхню призми.
2. Задача 2
Задано правильна трикутна піраміда, сторона основи якої 6
см, а бічна поверхня дорівнює 72 см2. Знайти апофему піраміди.
3. Задача 3
У правильній трикутній призмі сторона основи 12 см, а діагональ бічної грані – 17см. Знайти об’єм призми.
Завдання на період з 18.04 по 22.04 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 21.04
Tема : "Многогранники. Площі поверхонь та об’єми многогранників."
Переглянути відео за посиланням : https://www.youtube.com/watch?v=kIaPp6_EuSY
Опрацювати матеріал :
Домашнє задання : опрацювати теорію, виконати вправи
Цеглина має форму прямокутного паралелепіпеда. Фірма виготовляє цеглини розміром 20 * 10 * 5 см. Скільки контейнерів розміром 2* 2 * 1,5 м потрібно заготовити для перевезення 24000 цеглин?
Задача 2
Сторона основи правильної чотирикутної піраміди дорівнює 8 см, площа бічної поверхні− 80 см2. Знайдіть об'єм піраміди.
Задача 3
Висота правильної чотирикутної піраміди дорівнює 3 см, а сторона її основи − 12 см.Знайти довжину бічного ребра піраміди.
Дата 19.04
Tема : "Координати та вектори в просторі.."
Переглянути відео за посиланням :https://www.youtube.com/watch?v=ZUWssDatcs4
Опрацювати матеріал :
Домашнє задання : опрацювати теорію, виконати вправи
Задано точки A(1; 2; 3), B(0; 1; 2), C(1; 2; 0), D(1; 0; 2). Яка із цих точок лежить у площині XOZ?.
Задано точки A(1; 2; 3), B(0; 1; 2), C(1; 0; 0), D(1; 0; 2). Яка із цих точок лежить у площині УOZ?.
Задано точки A(1; 2; 3), B(0; 1; 2), C(1; 0; 0), D(1; 0; 2). Яка з цих точок лежить: на осі ОХ?
Задано точки А (1; 2; 3), В (2; 3; 1), С (3; 1; 2). Знайдіть периметр трикутника AВС.
Знайдіть координати точки С — середини відрізка АВ, якщо А (1; 2; 3), В (-3; 2; 1)
Знайдіть координати вектора АВ,якщо А(1;3;5), В(4;3;6)
Знайдіть модуль вектора а(-3;0;4)
Знайдіть суму векторів ̅а(3;1;-2) і ̅в(3;-2;5)
Знайдіть координати вектора 4̅а, якщо ̅а(1;-3; 4)
Знайдіть скалярний добуток векторів ̅а(1;2;-3) і ̅в(-8;2;4)
Завдання на період з 11.04 по 15.04 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 14.04
Tема : "Перпендикулярність прямих і площин у просторі."
Переглянути відео за посиланням :https://www.youtube.com/watch?v=bkFiAQmX8q0
Опрацювати матеріал :
Перпендикулярність прямої і площиниПряма, що перетинає площину, називається перпендикулярною цій площині, якщо вона перпендикулярна кожній прямій, яка лежить у цій площині.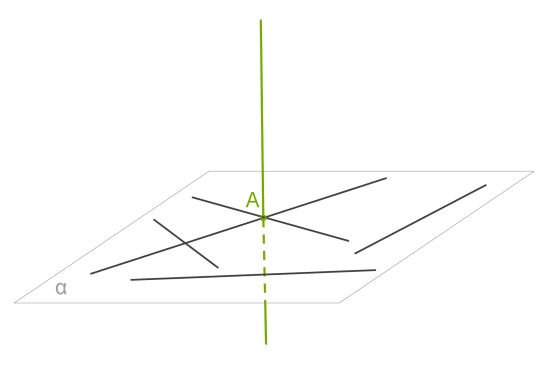 Перпендикулярність прямої і площини позначається як
Перпендикулярність прямої і площини позначається як a⊥α .Через будь-яку точку простору проходить пряма перпендикулярна даній площині, і до того ж тільки одна.Ознака перпендикулярності прямої і площини.
Якщо пряма перпендикулярна двом прямим, що перетинаються у площині, то вона перпендикулярна цій площині. 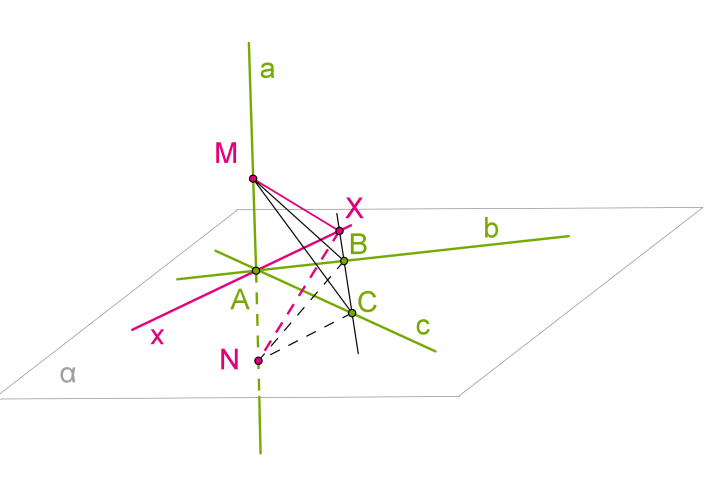 Доведення: Нехай
Доведення: Нехай a — пряма, перпендикулярна прямим b і c у площині. Проведемо пряму a через точку A перетину прямих b і c . Доведемо, що пряма a перпендикулярна площині, тобто кожній прямій в цій площині. 1. Проведемо довільну пряму x через точку A в площині і покажемо, що вона перпендикулярна прямій a . Проведемо в площині довільну пряму, що не проходить через точку A і перетинає прямі b , c і x . Нехай точками перетину будуть B , C і X . 2. Відкладемо на прямій a від точки A в різні сторони рівні відрізки AM і AN . 3. Трикутник MCN рівнобедрений, оскільки відрізок AC є висотою за умовою теореми і медіаною з побудови (AM=AN ). З тієї ж причини трикутник MBN теж рівнобедрений. 4. Отже, трикутники MBC і NBC рівні за трьома сторонами. 5. З рівності трикутників MBC і NBC випливає рівність кутів MBX і NBX і, отже, рівність трикутників MBX і NBX за двома сторонами та кутом між ними. 6. З рівності сторін MX і NX цих трикутників випливає, що трикутник MXN рівнобедрений. Тому його медіана XA є також висотою. А це і означає, що пряма x перпендикулярна a . За визначенням пряма a перпендикулярна площині.
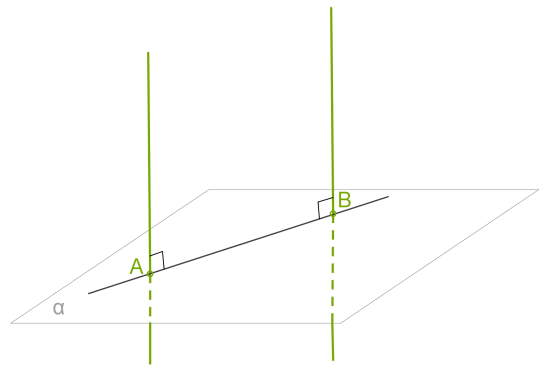
Властивості перпендикулярних прямої та площини.1. Якщо площина перпендикулярна одній з двох паралельних прямих, то вона перпендикулярна й інший.2. Дві прямі, перпендикулярні одній і тій же площині, паралельні.

Якщо пряма перпендикулярна двом прямим, що перетинаються у площині, то вона перпендикулярна цій площині.


Домашнє задання : опрацювати теорію
Дата 12.04
Tема : "Взаємне розміщення прямих і площин у просторі."
Переглянути відео за посиланням :https://www.youtube.com/watch?v=DxlZf1gyhh0
Опрацювати матеріал :
Перпендикулярні прямі в просторіДві прямі називаються перпендикулярними, якщо кут між ними дорівнює 90°.У просторі перпендикулярними називають не тільки прямі, що перетинаються, а й мимобіжні прямі, тому що ми кажемо про кут, який можуть утворити ці прямі, якщо їх розташувати в одній площині. Так само як і в площині, в просторі перпендикулярні прямі a і b позначають a⊥b .Якщо одна з двох паралельних прямих перпендикулярна до третьої прямої, то й інша перпендикулярна до цієї прямої.
Паралельність прямої та площини.Відповідно до аксіом, якщо дві точки прямої містяться в деякій площині, то пряма лежить у цій площині. З цього виходить, що можливі три випадки взаємного розташування прямої та площини у просторі:1) пряма лежить в площині;2) пряма і площина мають тільки одну спільну точку (пряма і площина перетинаються);3) пряма і площина не мають спільних точок.Пряма і площина називаються паралельними, якщо вони не мають спільних точок.Теорема 5 «Ознака паралельності прямої і площини».
Якщо пряма, що не лежить у даній площині, паралельна будь-якій прямій з цієї площини, то ця пряма паралельна даній площині.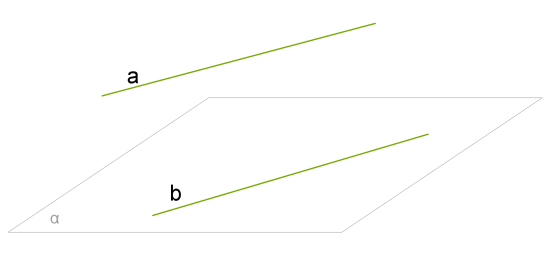 Доведення:
Доведення:
Доведення проведемо від супротивного. Нехай a не паралельна площині α , тоді пряма a перетинає площину в якійсь точці A . Причому A не лежить на b , оскільки a∥b . Відповідно до ознаки прямих, що перетинаються, прямі a і b перетинаються.
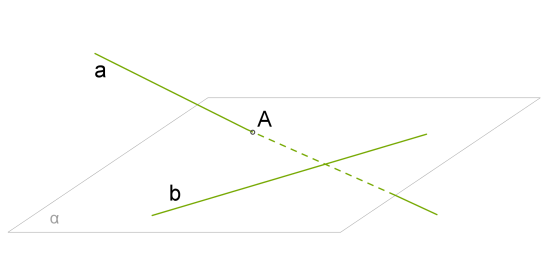 Ми дійшли до суперечності. Оскільки
Ми дійшли до суперечності. Оскільки a∥b , вони не можуть перетинатися. Отже, пряма a паралельна площині α .Зверни увагу!Наступні дві теореми дуже часто використовуються при розв'язанні задач.Теорема 6.
Якщо площина β проходить через дану пряму a , паралельну площині α , і перетинає цю площину по прямій b , то b∥a .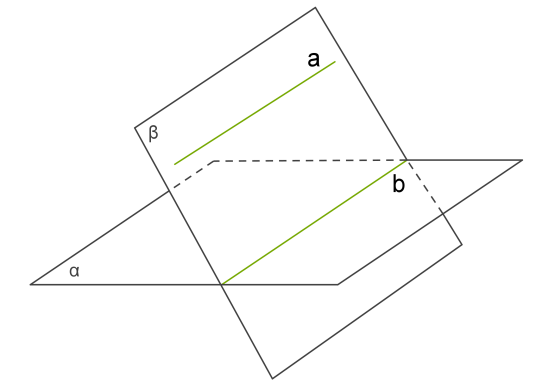 Зверни увагу!Пряму
Зверни увагу!Пряму b іноді називають відбитком площиниβ на площиніα .Теорема 7.
Якщо одна з двох паралельних прямих a∥b є параллельною даній площині α , то друга пряма або є параллельною цій площині, або лежить у цій площині.
Якщо пряма, що не лежить у даній площині, паралельна будь-якій прямій з цієї площини, то ця пряма паралельна даній площині.

Доведення проведемо від супротивного. Нехай

Якщо площина

Якщо одна з двох паралельних прямих
Домашнє задання : опрацювати теорію, виконати вправи :
Запитання 1Скільки площин проходить через дану точку простору перпендикулярно до даної прямої?
Запитання 2Якщо пряма, перпендикулярна до однієї з двох паралельних площин, то вона ...
Запитання 3Із точки поза площиною проведено до неї перпендикуляр довжиною 6см і похилу довжиною 9 см. Знайти довжину проекції похилої.
Запитання 4Перпендикуляром до площини називають...
Запитання 5Якщо дві площини перпендикулярні до третьої площини ,то їх лінія перетину з цією площиною...
Запитання 6
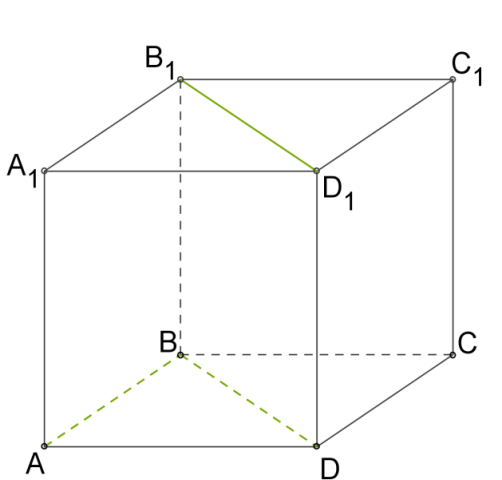
Дано прямокутний паралелепіпед АВСDА1В1С1D1 (див. рис.). Зазначте пряму, що є мимобіжною з прямою А1В1.
Запитання 7Площина α перетинає сторони АВ і АС трикутника АВС в точках М і N відповідно, ВС ∥ α. Знайдіть ВС, якщо
МN = 1 см; ВМ ∶ МА = 3 ∶ 1.
Скільки площин проходить через дану точку простору перпендикулярно до даної прямої?
Якщо пряма, перпендикулярна до однієї з двох паралельних площин, то вона ...
Із точки поза площиною проведено до неї перпендикуляр довжиною 6см і похилу довжиною 9 см. Знайти довжину проекції похилої.
Перпендикуляром до площини називають...
Якщо дві площини перпендикулярні до третьої площини ,то їх лінія перетину з цією площиною...

Дано прямокутний паралелепіпед АВСDА1В1С1D1 (див. рис.). Зазначте пряму, що є мимобіжною з прямою А1В1.
Площина α перетинає сторони АВ і АС трикутника АВС в точках М і N відповідно, ВС ∥ α. Знайдіть ВС, якщо
МN = 1 см; ВМ ∶ МА = 3 ∶ 1.
Завдання на період з 04.04 по 08.04 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 07.04
Tема : "Взаємне розміщення прямих і площин у просторі."
Переглянути відео за посиланням :https://www.youtube.com/watch?v=4TYp7Dn8dcs
Опрацювати матеріал :
В просторі ми можемо уявити ситуацію, коли дві прямі не перетинаються і не є паралельними.



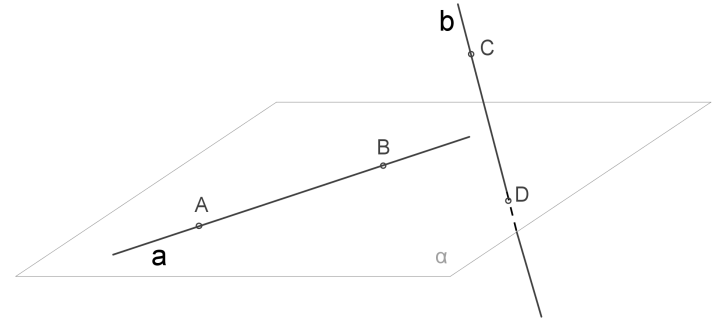
2. Це означає, що площина проходить через пряму
3. Маємо протиріччя умові теореми, отже пряма
Теорема доведена.
1. Паралельні
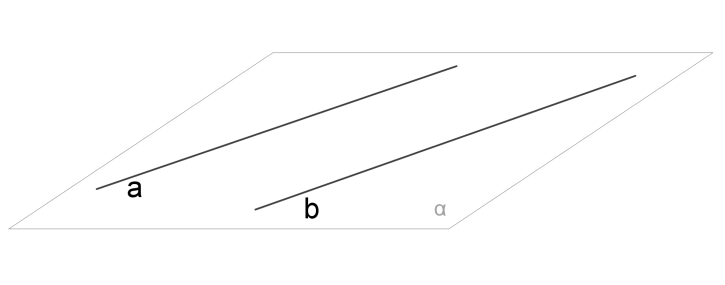
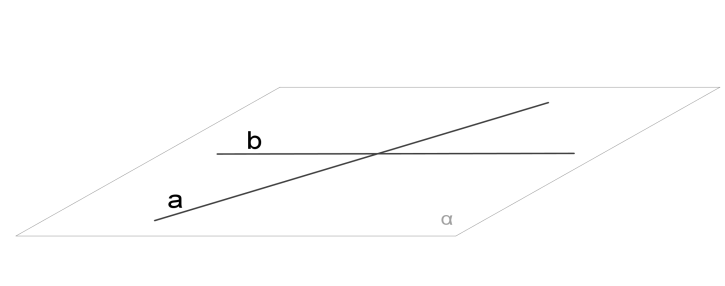
3. Мимобіжні
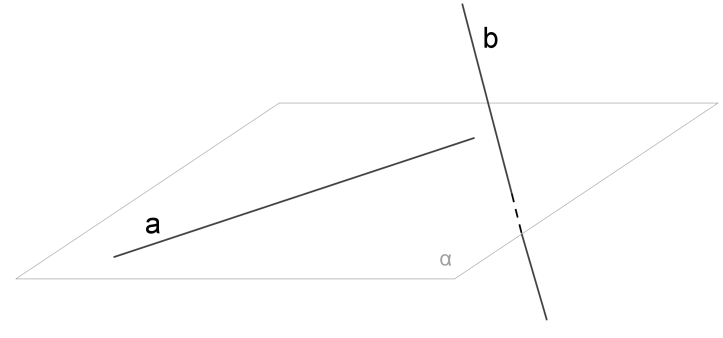
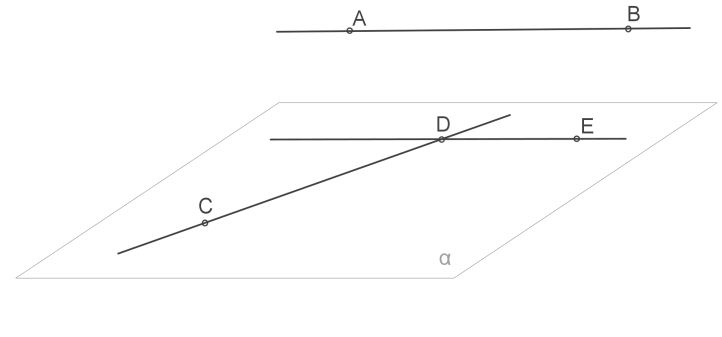
2. Через прямі, що перетинаються
3. Так як пряма
Теорема доведена.
2. Кутом між двома прямими, що перетинаються, називають величину меншого з кутів, утворених цими прямими. Якщо всі кути рівні, то ці прямі перпендикулярні (утворюють кут
3. Кутом між двома мимобіжними прямими називають кут між двома прямими, що перетинаються, відповідно паралельними мимобіжним прямим.
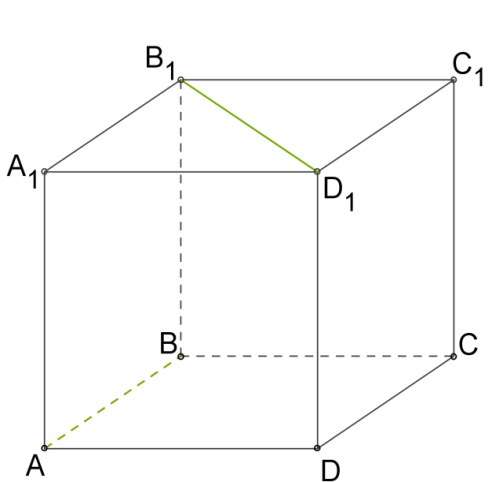
Домашнє задання : Дати відповіді на питання :
Домашнє задання : Дати відповіді на питання :
1. Двi прямi, що лежать в однiй площинi i не перетинаються…
2. Мимобiжними називаються прямi…
3. Двi прямi, паралельнi третiй…
4. Через пряму i точку, що не лежить на цiй прямiй, можна…
5. Через двi прямi, що перетинаються, можна…
6. Вiдрiзок, що сполучає середини двох сторiн трикутника,
називається…
7. Середня лiнiя трикутника паралельна…
8. Вiдрiзок, що сполучає середини бiчних сторiн трапецiї,
називається…
9. Середня лiнiя трапецiї дорiвнює…
10.
Якщо
два кути одного трикутника дорiвнюють двом кутам іншого трикутника, то цi трикутники…
Дата 05.04
Tема : "Корекція знань ,умінь та навичок"
Опрацювати презентацію : https://prezi.com/c5zr0ouydsoi/presentation/
Домашнє задання : Параграф 11- 14 повторити
№ 2 :
Висота конуса дорівнює 8 см, а радіус основи конуса на 4 см менший за його твірну. Знайти площу бічної поверхні конуса.
Завдання на період з 28.03 по 31.03 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 31.03
Tема : "Контрольна робота з теми : Обєми та площі поверхонь геометричних тіл"
Домашнє задання : Параграф 11- 14 повторити
Дата 29.03
Tема : "Узагальнення та систематизація знань ,умінь і навичок учнів з теми : Обєми та площі поверхонь геометричних тіл"
Завдання на період з 21.03 по 25.03 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 24.03
Tема : "Розвязування задач. Самостійна робота"
Виконати самостійну роботу за посиланням : https://docs.google.com/forms/d/e/1FAIpQLSfoCFyhtfO4HVz-RC5-Pg9y9yqCRTp1YOahsgIkTLzIngdocg/viewform?usp=sf_link
Домашнє задання : Параграф 14 повторити
Дата 22.03
Tема : "Площа сфери"
Опрацювати матеріал :https://www.youtube.com/watch?v=yXbgTQ6I2JM&ab_channel=%D0%A2%D0%BE%D0%BF%D0%A8%D0%BA%D0%BE%D0%BB%D0%B0
Кулею називається тіло, яке утворене з усіх точок простору, що знаходяться на відстані, що не більше даної, від даної точки. Поверхню кулі називається сферою.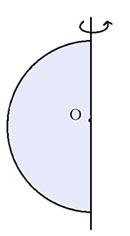

Переріз кулі площиною, що проходить через центр кулі, називається великим колом.
Для спрощення, зазвичай, малюється не куля, а велике коло кулі.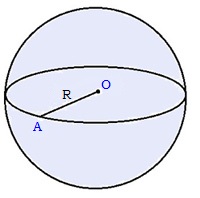
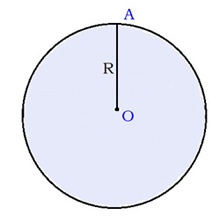
Зображення куліOA=R Велике колоOA=R
Площа поверхні кулі (тобто сфери) обчислюється за формулою S(сфери)= 4⋅π⋅R2 , де R — радіус кулі.Кульовим сегментом називається частина кулі, що відсікається від нього площиною.Малюється велике коло.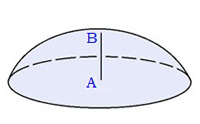
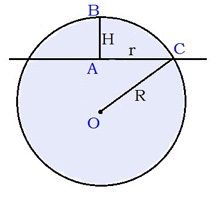
Коло з центром A — основа кульового сегмента. AC=r — радіус основи кульового сегмента,
AB=H — висота кульового сегмента,
OC=R — радіус кулі.
Площа сферичного сегмента обчислюється за формулою S(сегм.)= 2πRH
 |  |
Для спрощення, зазвичай, малюється не куля, а велике коло кулі.
 |  |
Зображення кулі | Велике коло |
 |  |
Домашнє задання : Параграф 14 пункти 4 , виконати вправи : 14.12, 14.30, 14.32
Завдання на період з 14.03 по 18.03 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 17.03
Tема : "Площа бічної та повної поверхонь циліндра ,конуса"
Опрацювати матеріал :https://www.youtube.com/watch?v=8avE71stuHk
Опрацювати матеріал :
https://www.youtube.com/watch?v=fRY2PWykmzs
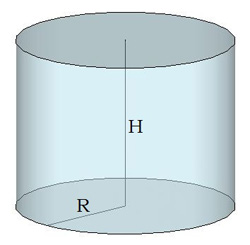
Площа поверхні циліндра утворена з площі бічної поверхні і площі основ циліндра. Площа бічної поверхні циліндраS(біч.)= 2πRH ,де R — радіус циліндра,H — висота циліндра.

Розгортка бічної поверхні циліндра на площині — прямокутник.
Одна сторона прямокутника є висотою циліндра.AB=H Друга сторона прямокутника є довжиною кола основи циліндра. AD= 2πR
Основи циліндра — кола. S(кола)= πR2 . Площа повної поверхні циліндра дорівнює:S(повн.)=2S(осн.)+S(біч.)= 2πR2 + 2πRH
Площа поверхні конуса складається з площі бічної поверхні конуса та площі основи (круга). 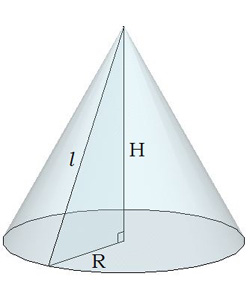
Площа бічної поверхні конуса обчислюється за формулою:S(бок.)=πRl де R — радіус конуса,l — твірна конуса. Площа основи конуса обчислюється за формулою S(повн.) = S(біч.) + S(кола) = S(кола) =πR2 Площа повної поверхні конуса обчислюється за формулою S(повн.) =S(біч.) +S(кола) =πRl+πR2
Площа поверхні циліндра утворена з площі бічної поверхні і площі основ циліндра. Площа бічної поверхні циліндра де |
Розгортка бічної поверхні циліндра на площині — прямокутник. Одна сторона прямокутника є висотою циліндра. Друга сторона прямокутника є довжиною кола основи циліндра. |
Площа бічної поверхні конуса обчислюється за формулою: де Площа повної поверхні конуса обчислюється за формулою |
Домашнє задання : Повторити параграф 14 , виконати вправи : 14.2, 14.4, 14.6
Дата 14.03
Тема : "Розвязування задач "
Опрацювати матеріал :https://www.youtube.com/watch?v=_gMrZt5PF1k
Домашнє задання : Повторити параграф 13 , виконати вправи : 13.10 , 13.18
Завдання на період з 24.02 по 25.02 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 24.02
Тема : "Обєм кулі "
Опрацювати матеріал :https://www.youtube.com/watch?v=VQngC0qNRCo
Кулею називається тіло, яке утворене з усіх точок простору, що знаходяться на відстані, що не більше даної, від даної точки. Поверхню кулі називається сферою. 

Переріз кулі площиною, що проходить через центр кулі, називається великим колом.
Для спрощення, зазвичай, малюється не куля, а велике коло кулі. 

Зображення куліOA=R Велике колоOA=R
Площа поверхні кулі (тобто сфери) обчислюється за формулою S(сфери)= 4⋅π⋅R2 , де R — радіус кулі.Об'єм кулі обчислюється за формулою V(кулі)= 4⋅π⋅R33 , де R — радіус кулі.Кульовим сегментом називається частина кулі, що відсікається від нього площиною.Малюється велике коло.

Коло з центром A — основа кульового сегмента. AC=r — радіус основи кульового сегмента,
AB=H — висота кульового сегмента,
OC=R — радіус кулі. Площа сферичного сегмента обчислюється за формулою S(сегм.)= 2πRH Об'єм кульового сегмента обчислюється за формулоюV(сегм.)= πH2⋅(R−H3) , де R — радіус кулі, H — висота кульового сегмента. У формулах для сегмента не використовується радіус основи сегмента, а використовується радіус кулі.
 |  |
Для спрощення, зазвичай, малюється не куля, а велике коло кулі.
 |  |
Зображення кулі | Велике коло |
 |  |
Домашнє задання : Опрацювати параграф 13 , виконати вправи : 13.2 , 13.4, 13.6, 13.8
Завдання на період з 11.10 по 13.10
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер 0960813579
Дата 11.10 Тема уроку : "Піраміда. Правильна піраміда"
Опрацювати матеріали за посиланням :https://www.youtube.com/watch?v=vBYN5MdMbgU
Піраміда, основою якої є правильний багатокутник, а вершина якої проектується в центр основи, називається правильною пірамідою. Бічні грані правильної піраміди — рівні трикутники.
Висота бічної грані правильної піраміди називається апофемою. Правильна трикутна піраміда, у якої всі ребра рівні, називається тетраедром.
Всі грані тетраедра — рівні рівносторонні трикутники. У середній школі потрібно вміти розв'язувати задачі, де задана
- правильна трикутна піраміда;
- правильна чотирикутна піраміда;
- правильна шестикутна піраміда. 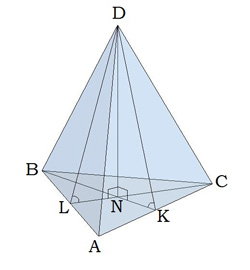 Правильна трикутна піраміда Основа правильної трикутної піраміди — рівносторонній трикутник.
Правильна трикутна піраміда Основа правильної трикутної піраміди — рівносторонній трикутник.
Вершина піраміди проектується в точку перетину медіан.
Запам'ятай:BN:NK=2:1 KD — апофема,∠ NKD і ∠ NLD — двогранні кути при основі піраміди,∠ DCN і ∠ DBN — кути між бічним ребром і площиною основи піраміди. 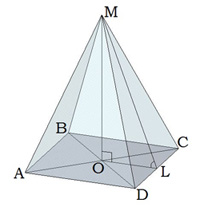 Правильна чотирикутна піраміда Основа правильної чотирикутної піраміди — квадрат.
Правильна чотирикутна піраміда Основа правильної чотирикутної піраміди — квадрат.
Вершина піраміди проектується в точку перетину діагоналей основи (квадрата).ML — апофема,∠ MLO — двогранний кут при основі піраміди,∠ MCO — кут між бічним ребром і площиною основи піраміди. 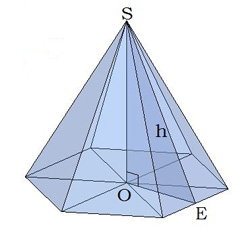 Правильна шестикутна піраміда Основа правильної шестикутної піраміди — правильний шестикутник.
Правильна шестикутна піраміда Основа правильної шестикутної піраміди — правильний шестикутник.
Вершина піраміди проектується в точку перетину діагоналей основи (шестикутника).SE=h — апофема,∠ OES — двогранний кут при основі піраміди.Формули. Для обчислення площі бічної поверхні правильної піраміди існують дві формули:Sб=12Pоснови⋅hіSб=Sосновиcosϕ , де P — периметр основи, h — апофема, ϕ — двогранний кут при основі. Об'єм піраміди V= 13Sосн⋅H , де H — висота піраміди.Зверни увагу!Не плутай h — апофему з H — висотою піраміди!
Висота бічної грані правильної піраміди називається апофемою.
Всі грані тетраедра — рівні рівносторонні трикутники.
- правильна трикутна піраміда;
- правильна чотирикутна піраміда;
- правильна шестикутна піраміда.
Вершина піраміди проектується в точку перетину медіан.
Запам'ятай:
Вершина піраміди проектується в точку перетину діагоналей основи (квадрата).
Вершина піраміди проектується в точку перетину діагоналей основи (шестикутника).
Домашнє задання : Опрацювати параграф 3 , виконати вправи : 3,4 , 3.6, 3.8
Завдання на період з 04.10 по 08.10
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер 0960813579
Дата 07.10 Тема уроку : "Площа бічної та повної поверхонь призми"
Опрацювати матеріали за посиланням :https://www.youtube.com/watch?v=7XtWWEnKvUQ
Ознайомитись з матеріалом :
Площею бічної поверхні призми називається сума площ усіх бічних граней призми.Площа бічної поверхні прямої призми Sбіч.=Pосн.⋅H ,де H — висота призми. Площа повної поверхні призми — сума площ всіх граней призми.
Вона утворена з площі бічної поверхні і площі основ Sповн.=Sбіч.+2⋅Sосн. Всі грані куба — квадрати, тому раціональніше використовувати формулу Sповн.пов.куба=6⋅a2 Об'єм прямої призми знаходиться за формулою:V=Sосн.⋅H Для прямокутного паралелепіпеда можна використовувати формулу V=abc , де a , b , c — виміри прямокутного паралелепіпеда (довжина, ширина, висота). Для куба використовується формула V=a3 , де a — ребро куба. Основою призми може бути будь-який n -кутник, тому важливо знати формули обчислення їх площ.
Вона утворена з площі бічної поверхні і площі основ
Домашнє задання : Опрацювати параграф 1 пункт 4 , виконати вправи :1.12 , 1.34
Дата 05.10 Тема уроку : "Паралелепіпед"
Опрацювати матеріали за посиланням :https://www.youtube.com/watch?v=h61mYfXbwSw
Ознайомитись з матеріалом :
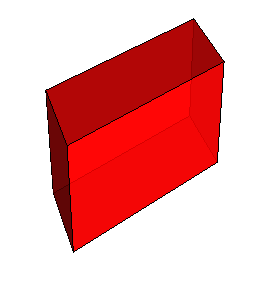
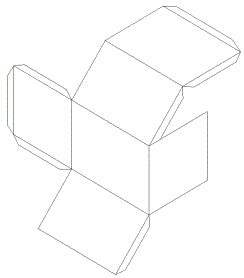 Паралелепіпедом називається багатогранник, у якого
Паралелепіпедом називається багатогранник, у якого6 граней — паралелограми. 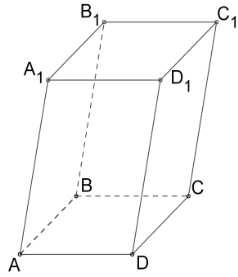 Рис. 4. У паралелепіпеда
Рис. 4. У паралелепіпеда 6 граней, 8 вершин і 12 ребер (Рис. 4.).
Дві грані паралелепіпеда, що мають спільне ребро, називаються суміжними, а не мають спільних ребер — протилежними. Зазвичай виділяють якісь дві протилежні грані і називають їх основами, а інші грані — бічними гранями паралелепіпеда. Ребра паралелепіпеда, що не належать основам, називають бічними ребрами. Відрізок, що з'єднує дві вершини, що не належать одній грані, називається діагоналлю паралелепіпеда (Рис. 5.).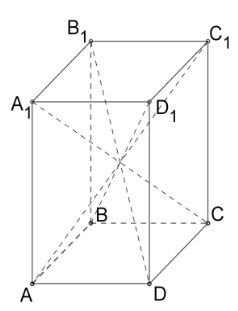 Рис. 5. Залежно від видів паралелограмів і їх розташування, виділяють різні види паралелепіпедів:
Рис. 5. Залежно від видів паралелограмів і їх розташування, виділяють різні види паралелепіпедів:
Паралелепіпеди можуть бути прямі і похилі. У прямих паралелепіпедів бокові грані прямокутники (Рис. 5.),у похилих — паралелограми (Рис. 4.). Прямий паралелепіпед, у якого основа також прямокутник, називається прямокутним паралелепіпедом. 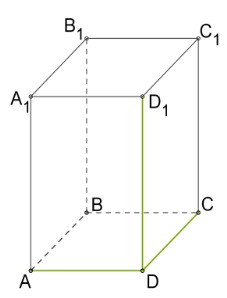 Рис. 6. Довжина непаралельних ребер прямокутного паралелепіпеда називається його лінійними розмірами (вимірами).У прямокутного паралелепіпеда три лінійні розміри
Рис. 6. Довжина непаралельних ребер прямокутного паралелепіпеда називається його лінійними розмірами (вимірами).У прямокутного паралелепіпеда три лінійні розміри DA , DC , DD1 (Рис. 6.).
Властивості паралелепіпеда:
— Протилежні грані паралелепіпеда рівні і паралельні. — Усі чотири діагоналі паралелепіпеда перетинаються в одній точці і діляться цією точкою навпіл. — Бічні грані прямого паралелепіпеда — прямокутники.




Паралелепіпеди можуть бути прямі і похилі.

— Протилежні грані паралелепіпеда рівні і паралельні.
Домашнє задання : Опрацювати параграф 2, виконати вправи : 2.7, 2.11
Завдання на період з 27.09 по 01.10
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер 0960813579
Дата 30.09 Тема уроку : "Розвязування задач"
Опрацювати матеріали за посиланням :https://www.youtube.com/watch?v=-ZypW3qbnFQ
Ознайомитись з матеріалом :
Многогранник або багатогранник дві грані якого рівні n-кутники, що лежать у паралельних площинах,а решта n граней – паралелограми, називають n-кутною призмою.
Многокутники, які рівні і лежать в паралельних площинах називають основами призми. В залежності від того, які многокутники лежать в основі призми, призми можуть бути: трикутними, чотирикутними, п'ятикутними, шестикутними і .т.д.
Сторони основ, називають ребрами основ
Усі паралелограми – це бічні грані.
Відрізки, що з'єднують вершини основ призми називають бічними ребрами призми. Усі біні ребра рівні і паралельні.
Призми поділяють на прямі та похилі.
Якщо бічні ребра призми перпендикулярні до площини основ то така призма називається прямою. Інші призми називаються похилими.
Правильною призмою називається пряма призма, в основі якої лежить правильний многокутник.
Висотою призми називається перпендикуляр, опущений із точки верхньої основи на площину нижньої основи. В прямій призмі висотою буде бічне ребро призми.
Переріз призми площиною, яка перетинає основи призми по діагоналі називають діагональним перерізом.
Діагоналлю призми називається відрізок, який з’єднує дві вершини, які не належать одній грані.
Площа бічної поверхні призми — це сума площ усіх її бічних граней
Площа поверхні призми знаходиться за формулою: площа бічної поверхні + 2 площі основ.
Переріз призми площиною, яка перетинає основи призми по діагоналі називають діагональним перерізом.
Діагоналлю призми називається відрізок, який з’єднує дві вершини, які не належать одній грані.
Площа бічної поверхні призми — це сума площ усіх її бічних граней
Площа поверхні призми знаходиться за формулою: площа бічної поверхні + 2 площі основ.
Домашнє задання : Повторити параграф 1 пункти 1-3 , виконати вправи : 1.118
Дата 28.09 Тема уроку : "Призма. Пряма і правильна призма"
Опрацювати матеріали за посиланням :https://www.youtube.com/watch?v=vpBF4sRd9b4
Ознайомитись з матеріалом :
ПризмаПризма — це многогранник, дві грані якого є рівними многокутниками, що знаходяться в паралельних площинах, а інші грані — паралелограми.Грані, які знаходяться в паралельних площинах, називаються основами призми, а інші грані — бічними гранями призми.
Залежно від основи призми бувають: 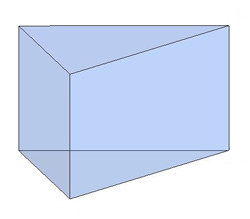 трикутними
трикутними 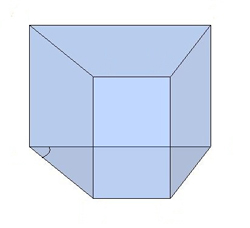
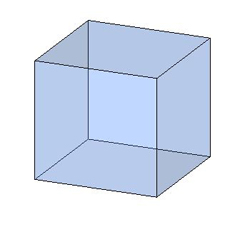 чотирикутними
чотирикутними 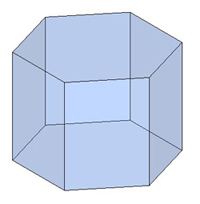 шестикутними та ін.Призма з бічними ребрами, перпендикулярними її основам, називається прямою призмою, як у попередніх малюнках.Пряма призма називається правильною, якщо її основи — правильні многокутники.
шестикутними та ін.Призма з бічними ребрами, перпендикулярними її основам, називається прямою призмою, як у попередніх малюнках.Пряма призма називається правильною, якщо її основи — правильні многокутники. Призма, бічні ребра якої не перпендикулярні основам, називається похилою призмою.
Призма, бічні ребра якої не перпендикулярні основам, називається похилою призмою.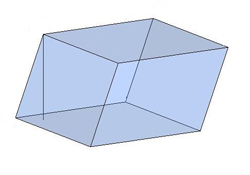 Відстань між основами призми називається висотою призми.Зверни увагу!Висота прямої призми збігається з боковим ребром.Висота похилої призми — це перпендикуляр, проведений між основами призми. Часто перпендикуляр проводять з однієї з вершин верхньої основи.Зверни увагу!Без додаткових умов неможливо визначити, в яку точку проектується висота похилої призми.
Відстань між основами призми називається висотою призми.Зверни увагу!Висота прямої призми збігається з боковим ребром.Висота похилої призми — це перпендикуляр, проведений між основами призми. Часто перпендикуляр проводять з однієї з вершин верхньої основи.Зверни увагу!Без додаткових умов неможливо визначити, в яку точку проектується висота похилої призми.
Залежно від основи призми бувають:




















Немає коментарів:
Дописати коментар