2021 -2022 н.р.
Завдання на період з 16.05 по .20.05 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 19.05
Тема : "Контрольна робота з теми : «Лінійні рівняння та їх системи»"
Виконати контрольну роботу за посиланням : https://docs.google.com/document/d/1nByOky0OY8_V3JIGJUMb5EnJ9niZNF23/edit?usp=sharing&ouid=114690071356165548445&rtpof=true&sd=true
Домашнє завдання :параграф 26-29 повторити , виконати контрольну роботу
Дата 16.05
Тема : "Узагальнення та систематизація знань, умінь і навичок учнів з теми : «Лінійні рівняння та їх системи»"
Опрацювати матеріал :
Реальна ситуація може бути описана математичною мовою у вигляді математичної моделі, тобто системи двох лінійних рівнянь із двома змінними. Складемо алгоритм для розв’язування текстових задач за допомогою системи рівнянь. Алгоритм розв’язування текстової задачі за допомогою системи рівнянь
1. Проаналізувати умову задачі (основні величини, зв’язки між ними, вимоги задачі).
2. Створити математичну модель (у вигляді таблиці, рисунка, тексту тощо).
3. Скласти систему рівнянь до задачі.
4. Розв’язати отриману систему рівнянь.
5. Проаналізувати отримані результати з огляду на умову задачі.
6. Записати відповідь.Приклад:Якщо чисельник дробу помножити на 2, а від знаменника відняти 2, то вийде 2.
Якщо від чисельника відняти 4, а знаменник помножити на 4, то вийде 112 . Знайди цей дріб. Розв'язання.
1. Аналізуємо умову задачі
Основні величини: звичайний дріб, над яким виконуються певні дії.
Аналіз дій, які виконуються над числами: нехай чисельник дробу дорівнює x, а знаменник — y.
Якщо чисельник дробу помножити на 2, а від знаменника відняти 2, то чисельник нового дробу дорівнюватиме 2x, а знаменник нового дробу дорівнюватиме y−2.
2. Створюємо математичну модель задачі.
За умовою причому обидві рівності виконуються одночасно. Тому потрібно скласти систему рівнянь. Знаючи, що новий дріб дорівнюватиме 2, утворюємо перше рівняння: 2xy−2=2. Якщо ж від чисельника відняти 4, а знаменник помножити на 4, тоді отримаємо друге рівняння: x−44y=112. 3. Складаємо систему рівнянь: ⎧⎩⎨⎪⎪2xy−2=2,x−44y=112.
4. Розв’язуємо отриману систему рівнянь методом алгебраїчного додавання. ⎧⎩⎨⎪⎪2xy−2=2,x−44y=112,⇔{2x=2(y−2),|:24y=12(x−4),|:4⇔{x=y−2,y=3(x−4),⇔{x−y=−2,−3x+y=−12,+{x−y=−2,−3x+y=−12,¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯−2x=−14,|:(−2)x=7.¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ Підставимо значення x−7 в будь-яке рівняння системи, наприклад, у друге і знайдемо y. −3x+y=−12,−3⋅7+y=−12,−21+y=−12,y=−12+21,y=9.¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ . 5. Аналізуємо отримані результати з огляду на умову задачі, записуємо відповідь.
Повернемося до позначень: чисельник дробу — x, а знаменник дробу — y. Отримаємо дріб 79. Відповідь: 79.
Розглянемо задачі, у яких системи двох лінійних рівнянь із двома змінними використовують як математичні моделі реальних ситуацій.Задачі на роботу
Якщо V — обсяг роботи, p — продуктивність праці, t — час, то: V=pt,p=Vt,t=Vp.
- Якщо працюють декілька людей, то продуктивності їхньої роботи додаються.
- Якщо обсяг роботи не зазначений, то його приймають за одиницю.
Задачі на рух
Якщо s — відстань, v — швидкість, t — час, то:
s=vt,v=st,t=sv. Задачі на рух по воді Якщо v — власна швидкість плавзасобу у стоячій воді, a — швидкість течії, то:
v+a — швидкість плавзасобу за течією;
v–a — швидкість плавзасобу проти течії.Схема задачі на купівлю товарів Ціна Кількість Вартість Ітовар x y A=xy ІІтовар
Схема задачі на запис числа Цифра десятків Цифра одиниць Значення числа Ічисло x y 10x+y ІІ число
Схема задачі на співвідношення чисельників і знаменників дробу Чисельник Знаменник Значення дробу Ідріб x y xy ІІдріб
Схема задачі на продуктивність праці (на роботу) Продуктивність праці Час роботи Обсяг роботи Іпрацівник p t V=pt ІІ працівник
Схема задачі на рух Швидкість Час Відстань Іоб'єкт v t s=vt ІІоб'єкт
Якщо від чисельника відняти
1. Аналізуємо умову задачі
Основні величини: звичайний дріб, над яким виконуються певні дії.
Аналіз дій, які виконуються над числами: нехай чисельник дробу дорівнює
Якщо чисельник дробу помножити на
За умовою причому обидві рівності виконуються одночасно. Тому потрібно скласти систему рівнянь. Знаючи, що новий дріб дорівнюватиме
4. Розв’язуємо отриману систему рівнянь методом алгебраїчного додавання.
Повернемося до позначень: чисельник дробу —
- Якщо працюють декілька людей, то продуктивності їхньої роботи додаються.
- Якщо обсяг роботи не зазначений, то його приймають за одиницю.
Ціна | Кількість | Вартість | |
І товар | |||
ІІ товар |
Цифра десятків | Цифра одиниць | Значення числа | |
І число | |||
ІІ число |
Чисельник | Знаменник | Значення дробу | |
І дріб | |||
ІІ дріб |
Продуктивність праці | Час роботи | Обсяг роботи | |
І працівник | |||
ІІ працівник |
Швидкість | Час | Відстань | |
І об'єкт | |||
ІІ об'єкт |
Завдання на період з 09.05 по .13.05 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 12.05
Тема : " Розв’язування вправ . Самостійна робота"
Опрацювати відео за посиланням :https://www.youtube.com/watch?v=M4ANVwIefJk
Виконати самостійну роботу за посиланням : :https://docs.google.com/document/d/1w8u3TgCOVSNoM2Rj835Fmr4MUhTT7r-0/edit?usp=sharing&ouid=114690071356165548445&rtpof=true&sd=true
Домашнє завдання :параграф 29 повторити , виконати самостійну роботу
Дата 09.05
Тема : " Розв’язування задач за допомогою систем лінійних рівнянь"
Опрацювати відео за посиланням :https://www.youtube.com/watch?v=yMxSmfEUMqQОпрацювати матеріал :
Розв′язування прикладних задач за допомогою системи лінійних
рівнянь
Види задач
1)Арифметичні задачі
2)Задачі на рух:
-рух по воді за течією і проти течії
-рух машин навздогін і назустріч
3)Задачі на зміну величини
4)Задачі на відсотки:
-на розчини і сплави
-на банківські розрахунки
5)Геометричні задачі
Схема розв′язування задач:
. 1) позначити деякі дві
невідомі величини змінними (наприклад, х і у);
2) за умовою задачі
скласти систему рівнянь;
3) розв’язати одержану
систему;
4) проаналізувати
знайдені значення змінних відповідно до умови задачі, дати відповідь на
запитання задачі;
5) записати відповідь
Наприклад :
За 7 шоколадних батончиків і 2 плитки шоколаду
заплатили 59 грн. Скільки коштує батончик і скільки плитка шоколаду, якщо
відомо, що три батончики дорожчі за одну плитку на 3 грн?
Р о з в ‘ я з а н н я. Нехай батончик
коштує х грн, а плитка шоколаду – у грн. Тоді сім батончиків коштують 7х грн, а
дві плитки шоколаду – 2у грн. Оскільки разом за таку кількість батончиків і
плиток шоколаду заплатили 59 грн, маємо рівняння: 7х + 2у = 59.
Вартість трьох батончиків складає 3х
грн, і вони дорожчі за плитку шоколада на 3 грн. Тому одержимо ще одне
рівняння: 3х – у = 3.
Щоб відповісти на запитання задачі,
ми маємо знайти такі значення х і у, які б задовольняли обидва рівняння, тобто
задовольняли систему рівнянь:
Розв’язавши цю систему, одержимо, що
х = 5; у = 12. Отже, вартість шоколадного батончика – 5 грн, а вартість плитки
шоколаду – 12 грн.
В і д п о в і д ь: 5 грн; 12 грн.
Розв′язування прикладних задач за допомогою системи лінійних
рівнянь
Види задач
1)Арифметичні задачі
2)Задачі на рух:
-рух по воді за течією і проти течії
-рух машин навздогін і назустріч
3)Задачі на зміну величини
4)Задачі на відсотки:
-на розчини і сплави
-на банківські розрахунки
5)Геометричні задачі
Схема розв′язування задач:
. 1) позначити деякі дві
невідомі величини змінними (наприклад, х і у);
2) за умовою задачі
скласти систему рівнянь;
3) розв’язати одержану
систему;
4) проаналізувати
знайдені значення змінних відповідно до умови задачі, дати відповідь на
запитання задачі;
5) записати відповідь
За 7 шоколадних батончиків і 2 плитки шоколаду
заплатили 59 грн. Скільки коштує батончик і скільки плитка шоколаду, якщо
відомо, що три батончики дорожчі за одну плитку на 3 грн?
Р о з в ‘ я з а н н я. Нехай батончик
коштує х грн, а плитка шоколаду – у грн. Тоді сім батончиків коштують 7х грн, а
дві плитки шоколаду – 2у грн. Оскільки разом за таку кількість батончиків і
плиток шоколаду заплатили 59 грн, маємо рівняння: 7х + 2у = 59.
Вартість трьох батончиків складає 3х
грн, і вони дорожчі за плитку шоколада на 3 грн. Тому одержимо ще одне
рівняння: 3х – у = 3.
Щоб відповісти на запитання задачі,
ми маємо знайти такі значення х і у, які б задовольняли обидва рівняння, тобто
задовольняли систему рівнянь:
Розв’язавши цю систему, одержимо, що
х = 5; у = 12. Отже, вартість шоколадного батончика – 5 грн, а вартість плитки
шоколаду – 12 грн.
В і д п о в і д ь: 5 грн; 12 грн.
Домашнє завдання :параграф 29 повторити , виконати вправи : № 1083,1087
Завдання на період з 02.05 по .06.05 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 05.05
Тема : " Лінійні рівняння та їх системи як математичні моделі текстових задач"
Опрацювати відео за посиланням :https://www.youtube.com/watch?v=62985hN_174
Опрацювати матеріал :
Розв’язування задач за допомогою систем лінійних рівнянь
Щоб розв’язати задачу складанням системи рівнянь, необхідно:
- Позначити дві невідомі величини буквами.
- Скласти буквені вирази за умовою задачі. За допомогою буквених виразів скласти систему двох рівнянь. Розв’язати систему рівнянь.
Надати величинам знайдених значень, перевірити відповідність умові задачі.
Записати у відповідь значення величин, про які йшлося в умові задачі.
Розв’яжемо задачу. Микола і Василь купували однакові зошити й олівці. Микола купив 15 зошитів і 3 олівці, заплативши за покупку 15 гривень. А Василь купив 20 зошитів і 5 олівців, заплативши за покупку 20 гривень 50 копійок. Скільки коштує один зошит та один олівець?
Розв’язання. Оскільки хлопці купували однакові зошити й олівці, можна позначити ціну зошита за х гривень, а ціну олівця — за у гривень. Тоді за 15 зошитів Микола заплатив 15х, а за 3 олівці – 3у. А вся покупка коштує 15х + 3у, що дорівнює 15.
Аналогічно визначаємо, що Василь заплатив за всю покупку 20х + 5у, що дорівнює 20,5. Складемо систему цих рівнянь і розв’яжемо її. Знайдемо значення х — 0,9, а у — 0,5.
Враховуючи, що за х позначали ціну зошита, робимо висновок, що зошит коштує 90 копійок.
Враховуючи, що за у позначали ціну олівця, робимо висновок, що олівець коштує 50 копійок.
Зверніть увагу!
Перед тим, як записати відповідь, необхідно зробити перевірку, чи мають смисл знайдені значення величин і чи справджується умова задачі при цих значеннях величин.
Розв’язування задач за допомогою систем лінійних рівнянь
Щоб розв’язати задачу складанням системи рівнянь, необхідно:
- Позначити дві невідомі величини буквами.
- Скласти буквені вирази за умовою задачі. За допомогою буквених виразів скласти систему двох рівнянь. Розв’язати систему рівнянь.
Надати величинам знайдених значень, перевірити відповідність умові задачі.
Записати у відповідь значення величин, про які йшлося в умові задачі.
Розв’яжемо задачу. Микола і Василь купували однакові зошити й олівці. Микола купив 15 зошитів і 3 олівці, заплативши за покупку 15 гривень. А Василь купив 20 зошитів і 5 олівців, заплативши за покупку 20 гривень 50 копійок. Скільки коштує один зошит та один олівець?
Розв’язання. Оскільки хлопці купували однакові зошити й олівці, можна позначити ціну зошита за х гривень, а ціну олівця — за у гривень. Тоді за 15 зошитів Микола заплатив 15х, а за 3 олівці – 3у. А вся покупка коштує 15х + 3у, що дорівнює 15.
Аналогічно визначаємо, що Василь заплатив за всю покупку 20х + 5у, що дорівнює 20,5. Складемо систему цих рівнянь і розв’яжемо її. Знайдемо значення х — 0,9, а у — 0,5.
Враховуючи, що за х позначали ціну зошита, робимо висновок, що зошит коштує 90 копійок.
Враховуючи, що за у позначали ціну олівця, робимо висновок, що олівець коштує 50 копійок.
Зверніть увагу!
Перед тим, як записати відповідь, необхідно зробити перевірку, чи мають смисл знайдені значення величин і чи справджується умова задачі при цих значеннях величин.
Домашнє завдання :параграф 29 опрацювати , виконати вправи : № 1079,1081
Дата 02.05
Тема : " Розв’язування систем двох лінійних рівнянь з двома змінними :способом додавання"
Опрацювати відео за посиланням :https://www.youtube.com/watch?v=_Afh0b23Lik
Опрацювати матеріал :
Розв’язання систем лінійних рівнянь із двома змінними
способом додавання
Алгоритм розв’язання систем лінійних
рівнянь із двома змінними способом додавання:
1. Помножте обидві частини рівнянь (рівняння) системи на
такі числа, щоб коефіцієнти при одній зі змінних стали протилежними числами
2. Додайте почленно ліві й праві частини рівнянь
3. Розв’яжіть здобуте рівняння з однією змінною
4. Знайдіть відповідне значення іншої змінної.
Розв’язання систем лінійних рівнянь із двома змінними
способом додавання
Алгоритм розв’язання систем лінійних
рівнянь із двома змінними способом додавання:
1. Помножте обидві частини рівнянь (рівняння) системи на
такі числа, щоб коефіцієнти при одній зі змінних стали протилежними числами
2. Додайте почленно ліві й праві частини рівнянь
3. Розв’яжіть здобуте рівняння з однією змінною
4. Знайдіть відповідне значення іншої змінної.
Домашнє завдання :параграф 28 повторити , виконати вправи : № 1052
Завдання на період з 25.04 по 29.04 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 28.04
Тема : " Розв’язування систем двох лінійних рівнянь з двома змінними :способом додавання"
Опрацювати відео за посиланням :https://www.youtube.com/watch?v=VS2ewVV1D4k
Опрацювати матеріал :
Домашнє завдання :параграф 28 повторити , виконати вправи : № 1050
Дата 25.04
Тема : " Розв’язування систем двох лінійних рівнянь з двома змінними :способом додавання"
Опрацювати відео за посиланням :https://www.youtube.com/watch?v=Wr7KoQPSizE
Опрацювати матеріал :
Алгоритм розв'язання системи двох лінійних рівнянь із двома змінними методом алгебраїчного додаванняЩоб розв’язати систему лінійних рівнянь методом додавання, треба:1) Дібравши «вигідні» множники, перетворити одне чи обидва рівняння системи так, щоб коефіцієнти при одній зі змінних стали протилежними числами;2) Додати почленно ліві й праві частини рівнянь, отриманих на першому кроці;3) Розв’язати рівняння з однією змінною, отримане на другому кроці;4) Підставити знайдене на третьому кроці значення змінної в будь-яке з рівнянь вихідної системи;5) Обчислити значення другої змінної та записати відповідь.Приклад:Завдання 1. Розв'язати систему рівнянь {3x−y=9,2x+y=11. Розв'язання. 1. Коефіцієнти при змінній y є протилежними числами тому додаємо почленно ліві й праві частини рівнянь.
+{3x−y=92x+y=11¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(3x−y)+(2x+y)=9+113x¯¯¯¯−y+2x¯¯¯¯+y=205⋅x=20x=20:5x=4¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ 2. Підставимо знайдене значення x у друге рівняння системи і знайдемо y.
2⋅x+y=112⋅4+y=118+y=11y=11−8y=3¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Відповідь: (4;3).
Завдання 2. Розв'язати систему рівнянь: {5x+6y=0,3x+4y=4. Розв'язання.1. У даній системі немає протилежних або рівних коефіцієнтів, тому, щоб позбутися змінної x, помножимо перше рівняння на 3, а друге на 5 і віднімемо почленно друге рівняння від першого.
{5x+6y=0,|⋅33x+4y=4;|⋅5⇔−{15x+18y=0,15x+20y=20;¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(15x+18y)−(15x+20y)=0−2015x+18y¯¯¯¯¯−15x−20y¯¯¯¯¯=−20,−2⋅y=−20,y=−20:(−2),y=10¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯.
2. Підставимо знайдене значення y в перше рівняння системи і знайдемо x.
5x+6y=0,5x+6⋅10=0,5x+60=0,5x=−60,x=−60:5,x=−12¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯.
Відповідь: x=−12,y=10.
Зверни увагу!Цей метод заснований на такому твердженні: якщо одне з рівнянь системи замінити на рівняння, отримане шляхом додавання лівих і правих частин рівнянь системи, то отримана система буде мати такі ж розв’язки, що й початкова.
Домашнє завдання :параграф 28 опрацювати , виконати вправи : № 1048
Завдання на період з 18.04 по 22.04 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 21.04
Тема : " Розв*язування систем двох лінійних рівнянь з двома змінними : способом підстановки.Самостійна робота"
Опрацювати відео за посиланням :https://www.youtube.com/watch?v=k5PxAz9NzKs
Опрацювати матеріал :
Домашнє завдання :параграф 27 повторити , виконати самостійну роботу за посиланням : https://docs.google.com/document/d/17KKb8h6Mcwu72qrgbi6b7j7SwRoPke67/edit?usp=sharing&ouid=114690071356165548445&rtpof=true&sd=true
Дата 18.04 Тема : " Розв*язування систем двох лінійних рівнянь з двома змінними : способом підстановки"
Опрацювати відео за посиланням :https://www.youtube.com/watch?v=8PGj2KMbZOM
Опрацювати матеріал : Розв’язати систему рівнянь 
1. Виражаємо одну змінну з якого-небудь рівняння системи через другу.

2. Замість цієї змінної підставляємо в друге рівняння системи утворений вираз.

3. Розв’язуємо отримане рівняння з однією змінною.

4. Знаходимо відповідне значення другої змінної.

5. Відповідь. (5; 2).
Розв’язати систему рівнянь ![]()
1. Виражаємо одну змінну з якого-небудь рівняння системи через другу.

2. Замість цієї змінної підставляємо в друге рівняння системи утворений вираз.
![]()
3. Розв’язуємо отримане рівняння з однією змінною.

4. Знаходимо відповідне значення другої змінної.

5. Відповідь. (5; 2).
Домашнє завдання :параграф 27 повторити ,
№ 1037
Завдання на період з 11.04 по 15.04 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 14.04 Тема : " Розв*язування систем двох лінійних рівнянь з двома змінними : способом підстановки"
Опрацювати відео за посиланням :https://www.youtube.com/watch?v=3f3itJf51RQ
Опрацювати матеріал : Алгоритм розв'язання системи двох рівнянь із двома змінними методом підстановкиЩоб розв'язати систему рівнянь способом підстановки, треба:
1. Виразити з якого-небудь її рівняння одну змінну через іншу;
2. Підставити в інше рівняння системи замість цієї змінної отриманий вираз;
3. Розв'язати утворене рівняння з однією змінною;
4. Знайти відповідне значення іншої змінної.
5. Записати відповідь.Приклад:Розв'язати систему рівнянь: {x−2y=3,5x+y=4.
1) З першого рівняння системи виражаємо змінну x через змінну y. Отримуємо: x−2y=3,x=3+2y; 2) Підставимо отриманий вираз замість змінної x у друге рівняння системи: 5⋅x+y=4,5⋅(3+2y)+y=4; 3) Розв'яжемо утворене рівняння з однією змінною, знайдемо y: 11y=−11,|:11
4) Знайдемо відповідне значення змінної x, підставивши значення змінної y, у вираз знайдений на першому кроці: x=3+2⋅y,x=3+2⋅(−1),x=3−2,x=1¯¯¯¯¯¯¯¯.
5) Відповідь: (1;−1) .
Зверни увагу!Способом підстановки можна розв’язувати будь-яку систему лінійних рівнянь із двома змінними, але найзручніше його використовувати, коли коефіцієнт при будь-якій змінній у рівнянні дорівнює 1.Зверни увагу!Іноді можна підставляти з одного рівняння системи в інше не значення окремої змінної, а значення цілого виразу: {x−2y=3,5(x−2y)+y=20. Можна значення x−2y з першого рівняння підставити у друге, отримавши рівняння з однією змінною: 5⋅3+y=20.
4) Знайдемо відповідне значення змінної
5) Відповідь:
Домашнє завдання :параграф 27 опрацювати ,
№ 1035(1-5)
Дата 11.04 Тема : " Розв*язування систем двох лінійних рівнянь з двома змінними : графічним способом"
Опрацювати відео за посиланням :https://www.youtube.com/watch?v=DBO0d5garC0
Опрацювати матеріал :
Розв’язування вправ по темі „Розв’язування систем двох лінійних рівнянь з двома змінними графічним способом і способом підстановки ”.
Повторимо для початку , як розв’язувати дані системи графічним способом і способом підстановки
Якщо треба знайти спільний розв’язок двох рівнянь із двома змінними, то кажуть, що ці рівняння утворюють систему рівнянь.
Позначення: 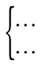
2. Розв’язком системи рівнянь із двома змінними називають пару значень змінних, при яких кожне рівняння перетворюється на правильну числову рівність.
Розв’язати систему рівнянь означає знайти всі її розв’язки або довести, що їх немає.
3. Щоб розв’язати систему лінійних рівнянь із двома змінними, можна скористатися графіками рівнянь. Такий спосіб називається графічним способом розв’язування систем рівнянь.
Щоб розв’язати систему рівнянь графічним способом, треба:
1. виконати рівносильні перетворення системи так, щоб було зручно побудувати графіки рівнянь системи;
2. побудувати графіки;
3. знайти координати точок (точки) перетину побудованих ліній. Ці координати і є розв’язками (розв’язком) системи рівнянь.
Приклад. Розв’яжіть графічно систему рівнянь 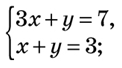

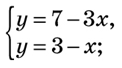
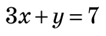
x
2
3
y
1
–2
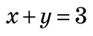
x
2
3
y
1
0
M(1;2) — точка перетину графіків рівнянь (рис. 1).

Рис. 1
1. Побудуємо графіки рівнянь системи в одній координатній площині.
2. Знайдемо координати точки перетину графіків рівнянь.
3. Якщо координати точки перетину цілі числа, то треба виконати перевірку, якщо ні, то дати приблизну відповідь.
Отже, графіком кожного рівняння системи лінійних рівнянь із двома змінними є пряма. Якщо прямі перетинаються, то система має єдиний розв’язок; якщо прямі не перетинаються, то система не має розв’язків; якщо прямі збігаються, то система має безліч розв’язків.
Розв’язування вправ по темі „Розв’язування систем двох лінійних рівнянь з двома змінними графічним способом і способом підстановки ”.
Повторимо для початку , як розв’язувати дані системи графічним способом і способом підстановки
Якщо треба знайти спільний розв’язок двох рівнянь із двома змінними, то кажуть, що ці рівняння утворюють систему рівнянь.
Позначення: 
2. Розв’язком системи рівнянь із двома змінними називають пару значень змінних, при яких кожне рівняння перетворюється на правильну числову рівність.
Розв’язати систему рівнянь означає знайти всі її розв’язки або довести, що їх немає.
3. Щоб розв’язати систему лінійних рівнянь із двома змінними, можна скористатися графіками рівнянь. Такий спосіб називається графічним способом розв’язування систем рівнянь.
Щоб розв’язати систему рівнянь графічним способом, треба:
1. виконати рівносильні перетворення системи так, щоб було зручно побудувати графіки рівнянь системи;
2. побудувати графіки;
3. знайти координати точок (точки) перетину побудованих ліній. Ці координати і є розв’язками (розв’язком) системи рівнянь.
Приклад. Розв’яжіть графічно систему рівнянь 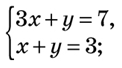

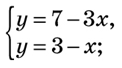
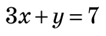
x | 2 | 3 |
y | 1 | –2 |
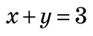
x | 2 | 3 |
y | 1 | 0 |
M(1;2) — точка перетину графіків рівнянь (рис. 1).

Рис. 1
1. Побудуємо графіки рівнянь системи в одній координатній площині.
2. Знайдемо координати точки перетину графіків рівнянь.
3. Якщо координати точки перетину цілі числа, то треба виконати перевірку, якщо ні, то дати приблизну відповідь.
Отже, графіком кожного рівняння системи лінійних рівнянь із двома змінними є пряма. Якщо прямі перетинаються, то система має єдиний розв’язок; якщо прямі не перетинаються, то система не має розв’язків; якщо прямі збігаються, то система має безліч розв’язків.
Домашнє завдання :параграф 26 повторити ,
№ 1011(3-4), 1017 (1-2)
Завдання на період з 04.04 по 07.04 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 07.04 Тема : " Розв*язування систем двох лінійних рівнянь з двома змінними : графічним способом"
Знайдемо дві пари значень змінних
Знайдемо дві пари значень змінних
Графіком рівняння
Домашнє завдання :параграф 26 опрацювати , № 1008, 1011(1-2)
Дата 04.04 Тема : " Лінійне рівняння з двома змінними та його графік"
Опрацювати матеріал :
- Лінійне рівняння з двома змінними та його графік
- Рівняння виду ах + bу = с, де а, b і с - деякі числа, називається лінійним рівнянням з двома змінними х і у.
- Графіком кожного лінійного рівняння з двома змінними є пряма.
- Якщо а, b і с не дорівнюють нулю, то пряма проходить під кутом до координатних осей і перетинає їх у двох точках.
- Якщо права частина лінійного рівняння з двома змінними дорівнює нулю, то пряма проходить через початок координат під кутом до координатних осей.
- Якщо коефіцієнт при змінній х = 0, а інші не дорівнюють нулю, то пряма паралельна осі х.
- Якщо всі коефіцієнти, окрім коефіцієнта при у, не дорівнюють нулю, то пряма паралельна осі у.
- Якщо всі коефіцієнти, окрім коефіцієнта при у, дорівнюють нулю, то пряма співпадає з віссю абсцис.
- Якщо всі коефіцієнти, окрім коефіцієнта при х, дорівнюють нулю, то пряма співпадає з віссю ординат.
- Якщо всі коефіцієнти дорівнюють нулю, то графіком будуть усі точки координатної прямої.
- Якщо всі коефіцієнти, окрім вільного члена, дорівнюють нулю, то не одержимо жодної точки.
Домашнє завдання :параграф 25 повторити , № 952, 962
Завдання на період з 28.03 по 31.03 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 28.03 Тема : " Лінійне рівняння з двома змінними та його графік"
Опрацювати матеріал :
Розв'язком рівняння ax+by=c називають будь-яку пару чисел (x ;y ), яка задовольняє це рівняння, тобто перетворює рівність зі змінними ax+by=c на правильну числову рівність.Приклад: Зобразити розв'язок лінійного рівняння з двома змінними x+y=3 точками у координатній площині xOy . Підберемо кілька розв'язків заданого рівняння, тобто кілька пар чисел, які задовольняють рівняння: (3,0),(2;1),(1,2),(0,3),(4;−1) . Побудуємо у координатній площині xOy ці точки.
Усі вони лежать на одній прямій t .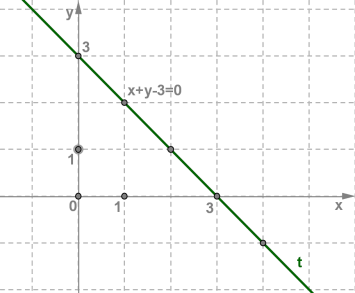 Пряма
Пряма t є графіком рівняння x+y=3 , або
пряма t є геометричною моделлю цього рівняння. Отже, якщо пара чисел (x ; y ) задовольняє рівнянняax+by=c , то точка М (x ;y ) належить прямій t .І навпаки, якщо точка М (x ;y ) належить прямій t , то пара чисел (x ;y ) задовольняє рівняння ax+by=c . Справедливою є така теорема:Якщо хоча б один з коефіцієнтів a,b лінійного рівняння ax+by=c відмінний від нуля, то графіком рівняння служить пряма лінія. Алгоритм побудови графіка рівняння ax+by=c , де a≠0,b≠0 1. Надати змінній x конкретне значення x=x1 ;з рівняння ax1+by=c знайти відповідне значення y=y1 .2. Надати змінній x інше значення x=x2 ;з рівняння ax2+by=c знайти відповідне значення y=y2 .3. Побудувати на координатній площині xOy точки: (x1;y1)(x2;y2) 4. Провести через ці дві точки пряму — вона і буде графіком рівнянняax+by=c Приклад:Побудувати графік рівняння x−2y−4=0 .Будемо діяти за алгоритмом.
1. Нехай x=0 , тоді отримаємо: 0−2y−4=0,−2y=4,y=4:(−2)y=−2 2. Нехай y=0 , тоді отримаємо:x−2⋅0−4=0x−4=0x=4 3. Побудуємо на координатній площині xOy отримані точки:(0;−2) та (4;0) 4. Проведемо через ці точки пряму. 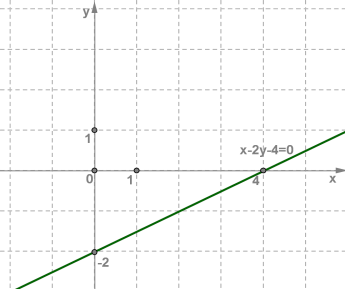 Вона і буде графіком лінійного рівняння
Вона і буде графіком лінійного рівняння x−2y−4=0
Усі вони лежать на одній прямій

пряма
1. Нехай

Домашнє завдання :параграф 25 , № 911, 914, 916
Дата 28.03 Тема : " Корекція знань,умінь і навичок.Лінійні рівняння з однією змінною"
Опрацювати матеріал :
Лінійне рівняння з однією змінною - рівняння виду ax = b, де a і b – деякі числа, x – змінна.
Розв’язки рівняння ax = b:

Приклади:
1) 3x =15 , x =15/3, х=5.
2) 0x = 0, x – будь-яке число ;
3) 0x = 10, рівняння розв’язків не має.
Завдання:
Розв'язати рівняння:
Приклади:
1) 3x =15 , x =15/3, х=5.
2) 0x = 0, x – будь-яке число ;
3) 0x = 10, рівняння розв’язків не має.
Домашнє завдання :параграф 1 пункт 2, № 35,38
Завдання на період з 21.03 по 25.03 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 24.03 Тема : " Контрольна робота з теми : "Функції""
Виконати контрольну роботу за посиланням : https://docs.google.com/document/d/1o1DKGUwtCOusiF3prHVhLCaHyXdCMFzS/edit?usp=sharing&ouid=114690071356165548445&rtpof=true&sd=true
Домашнє завдання :параграф 20-23 повторити
Дата 21.03 Тема : " Узагальнення та систематизація знань, умінь і навичок учнів з теми : "Функції""
Опрацювати матеріал :
1. Якщо кожному значенню змінної х з деякої множини відповідає єдине значення змінної у з іншої множини, то таку залежність називають функція
2. Значення
змінної, яку вибирають довільно називають незалежною або аргумент
3.Усі значення, яких може набувати аргумент називають область визначення функції
4. Змінна у
називають функція, значення функції
5. Усі
значення, яких набуває функція при аргументах, взятих з області визначення
функції, утворюють область значень
функції
6. Множина
усіх точок координатної площини, абсциси яких дорівнюють значенню аргументу, а
ординати — відповідним значенням функції, називається графіком функції
7. Функція задана формулою у = kх + b. Де k і b дані числа, називається лінійна функція
8. Коефіцієнти многочлена 3х3 – 2х2 – х – 2 — це 3; -2; -1; -2
9. Графіком лінійної функції є пряма
10. Дві перпендикулярні
координатні прямі, що перетинаються утворюють систему координат
11. Кожній точці координатної площини відповідає пара чисел, які називаються координатою точки
12. Скільки достатньо задати точок , щоб побудувати графік лінійної функції дві
Опрацювати матеріал : https://www.youtube.com/watch?v=ZZmx6p3pGzQ
Домашнє завдання :параграф 20-23 повторити , тести стор. 170-172
Завдання на період з 14.03 по 18.03 2022 року
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 17.03 Тема : " Розвязування вправ"
Опрацювати матеріал : https://www.youtube.com/watch?v=3f3M6cWVB2s
Домашнє завдання :параграф 23 повторити , № 859, 869
Дата 14.03 Тема : "Графік функції.Лінійна функція,її графік та властивості "
Опрацювати матеріал :https://www.youtube.com/watch?v=8RkMVKHUShI
Лінійна функція — це функція, яку можна задати формулоюy=kx+b , де x — незалежна змінна, k і b — деякі числа.Застосовуючи цю формулу, якщо відоме конкретне значення x , можна обчислити відповідне значення y .Нехай y=0,5x−2 .Тоді:якщо x=0 , тоді y=−2 ;якщо x=2 , тоді y=−1 ;якщо x=4 , тоді y=0 і т. д. Зазвичай ці результати оформлюють у вигляді таблиці: x 0 2 4 y −2 −1 0
x - незалежна змінна (або аргумент), y - залежна змінна.Графіком лінійної функції y=kx+b є пряма.
Щоб побудувати графік даної функції, нам достатньо мати координати двох точок, що належать графіку функції. Побудуємо на координатній площині xOy точки (0;−2) і (4;0) , оформлені у таблиці, і проведемо через них пряму. 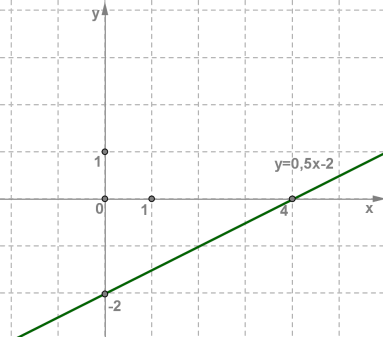 Багато реальних ситуацій описуються математичними моделями, що являють собою лінійні функції.Приклад:На складі було
Багато реальних ситуацій описуються математичними моделями, що являють собою лінійні функції.Приклад:На складі було 500 т вугілля. Щодня почали підвозити 30 т вугілля. Скільки вугілля буде на складі через 2 ; 4 ; 10 днів?Якщо пройшло x днів, то кількість y вугілля на складі (у тоннах) можна виразити формулою y=500+30x .Таким чином, лінійна функція y=30x+500 є математичною моделлю ситуації.За x=2 маємо y=560 ;за x=4 маємо y=620 ;за x=10 маємо y=800 Однак треба враховувати, що в цій ситуації x∈N . (натуральне число)Якщо лінійну функцію y=kx+b треба розглядати не за всіх значень x , а лише для значень x із деякої числової множини X , то пишуть y=kx+b,x∈X .Приклад:Побудувати графік лінійної функції:a) y=−2x+1,x∈[−3;2] b) y=−2x+1,x∈(−3;2) Складемо таблицю значень функції:x −3 2 y 7 −3
Позначимо на координатній площині xOy точки (−3;7) і (2;−3) та проведемо через них пряму. Далі виділимо відрізок, що з'єднує позначені точки. Цей відрізок і є графіком лінійної функції y=−2x+1,x∈[−3;2] .Точки (−3;7) і (2;−3) належать даному інтервалу (квадратні дужки) та на рисунку позначені темними кружечками. 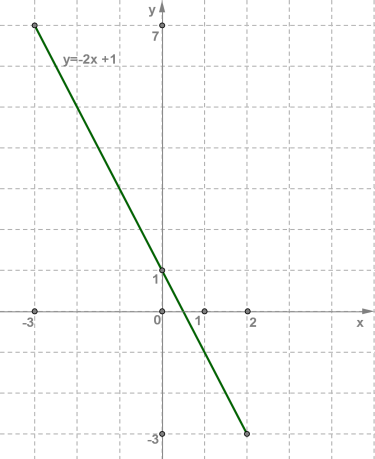 b) У другому випадку функція та сама, тільки значення
b) У другому випадку функція та сама, тільки значення x=−3 і x=2 не розглядаються, оскільки вони не належать інтервалу (−3;2) (круглі дужки).
Тому точки (−3;7) і (2;−3) на рисунку позначені світлими кружечками. 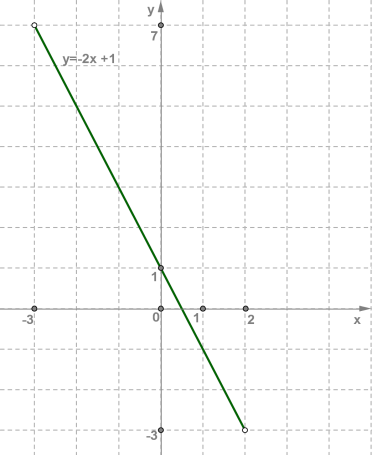 Розглядаючи графік лінійної функції на інтервалі, можна назвати найбільше і найменше значення лінійної функції. У випадкуa)
Розглядаючи графік лінійної функції на інтервалі, можна назвати найбільше і найменше значення лінійної функції. У випадкуa) y=−2x+1,x∈[−3;2] маємо, що yнайб =7 і yнайм =−3 ,b) y=−2x+1,x∈(−3;2) маємо, що ні найбільшого, ні найменшого значень лінійної функції немає, оскільки обидва кінці відрізка, у яких саме й досягалися найбільше і найменше значення, виключені з розгляду. У ході побудови графіків лінійних функцій, можна ніби «підніматися вгору» або «спускатися з гірки», тобто лінійна функція або зростає, або спадає.Якщо k>0 , тоді лінійна функція y=kx+b зростає;якщо k<0 , тоді лінійна функція y=kx+b спадає.Домашнє завдання :параграф 23 опрацюти , № 853, 855


Тому точки

Дата 24.02 Тема : "Розвязування вправ.Самостійна робота "
Опрацювати матеріал :https://www.youtube.com/watch?v=ZZmx6p3pGzQ
Виконати самостійну роботу :
1.
Функцію задано формулою у = 2х + 5.Знайдіть її значення при х= -3.
2.
Функцію задано формулою у = 4х – 8. Знайдіть значення
аргументу, при якому у = 32.
3.
Функцію задано за
допомогою таблиці. Знайдіть
значення функції при х = - 2, х = 2.
|
х |
-12 |
-6 |
|
|
|
|
24 |
-24 |
|
у |
|
|
2 |
3 |
-4 |
-6 |
|
|
Завдання на період з 11.10 по 13.10
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 11.10 Тема : "Одночлен.Піднесення одночлена до степеня"
Опрацювати матеріал :https://www.youtube.com/watch?v=2V7JN6peDhc
Піднесення одночленів до степеняПри піднесенні одночлена до степеня:
— кожен множник одночлена підноситься до степеня окремо;
— показники змінних множників одночлена (букви) перемножаються на показник степеня, до якого треба піднести одночлен.
Підносимо до степеня одночлен 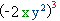 , отримуємо: 1) Одночлен розкладемо на множники.Запам'ятай: якщо степінь не вказаний, він дорівнює 1
, отримуємо: 1) Одночлен розкладемо на множники.Запам'ятай: якщо степінь не вказаний, він дорівнює 1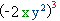 =
= 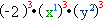 . 2) Кожен множник підноситься до степеня окремо.Запам'ятай: показники степеня змінних множиться на показник степеня, до якого підносимо одночлен
. 2) Кожен множник підноситься до степеня окремо.Запам'ятай: показники степеня змінних множиться на показник степеня, до якого підносимо одночлен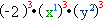 =
= 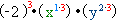 =
= 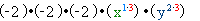 . 3) Підносячи від’ємний коефіцієнт до непарного степеня, отримуємо від’ємний результат:
. 3) Підносячи від’ємний коефіцієнт до непарного степеня, отримуємо від’ємний результат: 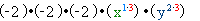
=−8⋅x3⋅y6=−8x3y6 .
— кожен множник одночлена підноситься до степеня окремо;
— показники змінних множників одночлена (букви) перемножаються на показник степеня, до якого треба піднести одночлен.
Домашнє завдання : параграф 7 опрацювати , № 266,272
Завдання на період з 04.10 по 08.10
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 07.10 Тема : "Властивості степеня з натуральним показником"
Опрацювати матеріал :https://www.youtube.com/watch?v=HcMHsyMjgtw
Розгляньмо приклад піднесення степеня до степеня:3дод.(a5)3=a5⋅a5⋅a5=a5+5+5=a5⋅3=a153множ. .
При піднесенні степеня до степеня показники степенів перемножуються,
а основа залишається без змін. (an)m=an⋅m
(де а — будь-яке число, n та m — натуральні числа).
Формула застосовується як зліва направо, так і справа наліво. Приклад:Завдання 1.Обчислити:а) (23)2
Розв’язання: (23)2=23⋅2=26=64 . б) 37:33
Розв’язання: 37:33=37−3=34=81 . Приклад:Завдання 2.Спростити вираз: (t6)4
Розв’язання: (t6)4=t6⋅4=t24 .Приклад: Завдання 3.Подати у вигляді п’ятого степеня. 1110
Розв’язання.Показаник степеня 10 можна представити у вигляді добутку, тоді1110=112⋅5=(112)5
an⋅am=an+man:am=an−m,n>m,a≠0(an)m=an⋅m
(де n та m — натуральні числа). На практиці нерідко застосовуються одночасно кілька властивостей.
Розгляньмо приклад: Приклад:Приклад.Обчислити: (54⋅5)357⋅56
Розв’язання:Виконаємо дії в чисельнику:1) 54⋅5=54⋅51=54+1=55 — застосували властивість an⋅am=an+m . 2) (55)3=55⋅3=515 — застосували властивість (an)m=an⋅m .
Виконаємо множення в знаменнику:3. 57⋅56=57+6=513 — застосували властивість an⋅am=an+m . Замінимо риску дробу діленням:4. 515:513=515−13=52 — застосували властивість an:am=an−m . 5. 52=25 Відповідь: 5 .
Домашнє завдання :параграф 6 опрацювати , № 212,237
а основа залишається без змін.
(де
Розв’язання:
Розв’язання:
Розв’язання:
Розв’язання.
(де
Розгляньмо приклад:
Розв’язання:
Дата 04.10 Тема : "Властивості степіня з натуральним показником"
Опрацювати матеріал :https://www.youtube.com/watch?v=ri2YPSakw9I
Розгляньмо приклад множення степенів з однаковими основами:a5⋅a3=a⋅a⋅...⋅a⋅a⋅a⋅a=a⋅a⋅...⋅a=a85разів3рази8разів
При множенні степенів з однаковими основами показники додаються,
а основа залишається без змін:an⋅am=an+m
(де а — будь-яке число, n і m — натуральні числа)
Зверни увагу!Не можна замінювати суму a6+a10 на a16 .
Формула застосовується як зліва направо, так і справа наліво. Приклад:Завдання 1.Обчислити:а) 53⋅5
Розв’язання: 53⋅5=53⋅51=53+1=54=625 . б) 34⋅32
Розв’язання%: 34⋅32=34+2=36=729 .
Приклад:Завдання 2.Спростити вираз. t12tt4
Розв’язання: t12tt4=t12⋅t1⋅t4=t12+1+4=t17 .Приклад: Завдання 3.Записати у вигляді добутку: 27
Розв’язання:Показник степеня 7 можна записати у вигляді доданка кількома способами:27=25+2=25⋅2227=26+1=26⋅21=26⋅2 .
При діленні степенів з однаковими основами від показника степеня діленого віднімається показник степеня дільника,а основа залишається без змін.an:am=an−m
(де a≠0 , n і m — натуральні числа, такі, що n>m ).
Зверни увагу!Не можна замінити різницю a15−a4 на a11 .
Формула застосовується як зліва направо, так і справа наліво. Приклад:Завдання 1.Обчислити.а) 53:5
Розв’язання: 53:5=53:51=53−1=52=25 . б) 37:33
Розв’язання: 37:33=37−3=34=81 .
Приклад:Завдання 2.Спростити вираз:t27t14
Розв’язання: t27t14=t27:t14=t27−14=t13 .Приклад: Завдання 3.Записати у вигляді частки: 27
Розв’язання:Показник степеня 7 можна записати у вигляді різниці кількома способами, наприклад:27=29−2=29:2227=28−1=28:21=28:2 . Домашнє завдання :параграф 6 опрацювати , № 207,210
а основа залишається без змін:
(де
Формула застосовується як зліва направо, так і справа наліво.
Розв’язання:
Розв’язання%:
Розв’язання:
Розв’язання:
(де
Формула застосовується як зліва направо, так і справа наліво.
Розв’язання:
Розв’язання:
Розв’язання:
Розв’язання:
Завдання на період з 27.09 по 01.10
Написати прізвище на кожній сторінці з виконаним завданням.
Сфотографувати кожну сторінку з виконаним завданням.
Відправити сфотографовану сторінку на вайбер або ел.пошту mosienko13.06@gmail.com
Завдання відправляти до кінця кожного тижня.
Запитання відсилати на вказану адресу або в вайбер : 0960813579
Дата 30.09 Тема : "Степінь з натуральним показником"
Опрацювати матеріал :https://www.youtube.com/watch?v=t8P27nSQuyk
снує короткий запис для множення числа кілька разів самого на себе, наприклад: 5⋅5⋅5⋅5⋅5⋅5⋅5=577разів Під an , де n=2,3,4,5,..., розуміють добуток n однакових множників,
кожним з яких є число a .Вираз an називають степенем, число a — основою степеня,
число n — показником степеня.Число n коротко ще називають натуральним показником, тому що це натуральне число (числа, які застосовуються під час рахунку предметів). Зверни увагу!a⋅a⋅a⋅...⋅a=annразів an — степінь з натуральним показником;a — основа степеня;n — показник степеня.Запис an читають так: «a в n -ному степені» або «a у степені n ».Запис a2 читають так: «a в квадраті» або «a у другому степені».Запис a3 читають так: «a в кубі» або «a у третьому степені». Приклад:Завдання 1.Використовуючи відповідні терміни, записати у вигляді степеня добуток: 3⋅3⋅3⋅3⋅3 .
Розв’язання.Оскільки дано добуток п’яти однакових множників, кожен з яких дорівнює 3 , маємо:
3⋅3⋅3⋅3⋅3=35 .35 — степінь;3 — основа степеня;5 — показник степеня. Приклад:Завдання 2.Обчислити: a) (−3)4
Розв’язання:(−3)4=(−3)⋅(−3)⋅(−3)⋅(−3)=81 . б)(411)2
Розв’язання.(411)2=411⋅411=4⋅411⋅11=16121 .в) 120=1⋅1⋅....⋅1=120раз09=0⋅0⋅....⋅0=09раз .Степенем числа a із показником 1 називають саме це число: a1=a 01=0(−25)1=−25(117)1=117 .
Домашнє завдання :параграф 5 опрацювати , № 163,165
кожним з яких є число
число
Розв’язання:
Розв’язання.
Дата 27.09 Тема : "Розвязування вправ"
Опрацювати матеріал :https://www.youtube.com/watch?v=-jcCTnmbOpI
Тотожність — це рівність, правильна при будь-яких значеннях змінних, що входять до неї.Якщо в дану буквену рівність підставити замість змінних будь-які допустимі значення, то має вийти правильна числова рівність. Тотожностями, наприклад, будуть основні властивості дій над числами:
a+b=b+a
(a+b)+c=a+(b+c)
ab=ba
(ab)c=a(bc)
a (b+c)=ab+ac
a+0=a
a ⋅ 0=0
a ⋅ 1=a
або формули скороченого множення, наприклад a2−b2=(a−b)(a+b) . Правильні числові рівності теж є тотожністю.
Приклад:Чи є тотожністю такі рівності:
1) 77+x=x+77
2) a−b=b−a
3) −5(−y)=5y
4) z2+z4=z6
Із цих рівностей тотожностями є рівності 1 та 3 . Які б числа ми в них не підставили замість змінних завжди вийдуть правильні числові рівності. 2 та 4 рівності не є тотожністю. Тому що ці рівності будуть виконуватися не за всіх допустимих значень змінних. Розглянемо 2 рівність a−b=b−a .
Наприклад, при значеннях a=14 та b=3 вийде такий результат:14−3=3−14 ;
11 ≠ −11 .Розглянемо 4 рівність z2+z4=z6 .При значенні z=2 вийде такий результат:22+24=26 4+16=64
20 ≠ 64 . Домашнє завдання :параграф 4 повторити , № 136,138
1)
2)
3)
4)
Із цих рівностей тотожностями є рівності
Наприклад, при значеннях








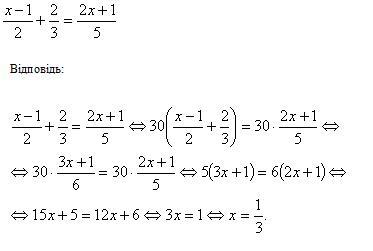



Немає коментарів:
Дописати коментар